APPENDICES
I. - Temps sidéral
II. - Table des valeurs approchées du temps sidéral à 0 heure de dix en dix jours
III. - Maisons
IV. - Sur la vraisemblance de certains écarts
V. - Textes divers intéressant l'astrologie - ISAIE
LA FONTAINE, L'horoscope
SAINT AUGUSTIN, Les confessions
I. - Temps sidéral
Donnons un exemple en nous bornant aux secondes rondes. Trouver l'heure sidérale d'un événement survenu à Paris le 1er août 1951, à 13 h. 52 min. exactement, heure française.
Le régime d'heure d'été étant en vigueur, et Paris appartenant au fuseau zéro, l'heure T. U. de l'événement est 12 h. 52 min.
Le 1er août 1951, à 0 heure T. U., l'heure sidérale est 20 h. 35 min. 11 sec. (donnée prise dans un annuaire). L' événement a lieu 12 h. 52 min. de T. U. plus tard, c'est-à-dire 12 h. 54 min. 7 sec. de temps sidéral plus tard. (L'addition de 2 min. 7 sec. tient compte de la différence entre temps solaire et temps sidéral: nous avons signalé l'écart quotidien de quatre minutes environ.) .
Cela étant, l'événemènt s'est produit à 20 h. 35 min. Il sec. + 12 h. 54 min. 7 sec. = 9 h. 29 min. 18 sec. en temps sidéral de Greenwich (24 h. ayant été retranchées).
Comme Paris se trouve à 9 min. 21 sec. de longitude à l'Est du méridien de Greenwich, l'heure sidérale locale de l'événement, que nous cherchons est, finalement, 9 h. 38 min. 39 sec.
On voit que ce calcul fait intervenir la longitude du lieu et la connaissance de l'heure sidérale à 0 heure T. U. au jour considéré.
En réalité, si l'on considère comme négligeable une erreur de plusieurs minutes, on peut abréger notablement l'opération.
Tout d'abord l'heure sidérale à 0 heure T. U. est toujours à peu près la même à une date donnée. Sa valeur passe de 0 heure à l'équinoxe d'automne (vers le 23 septembre) à 12 heures pour l'équinoxe de printemps et à 24 heures (0 heure) pour l'équinoxe d'automne suivant, croissant d'environ 3 min. 57 sec. par jour. Seules les discontinuités de notre calendrier et les incommensurabilités des périodes célestes entre elles introduisent un écart annuel qui peut ne pas dépasser ± 2 minutes. A cet écart près on peut donc se servir d'une petite table perpétuelle au lieu d'un annuaire.
D'autre part, la conversion de l'heure T. U. de l'événement en temps sidéral peut être négligée puisque la correction peut ne pas dépasser non plus ± 2 minutes (d'où la règle).
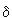 tg
tg 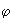
La définition classique des maisons, suivant Ptolémée, est la suivante:
« Chaque maison contient D/6 ou N/6 selon qu'elle est diurne ou nocturne.»
La figure (14) montre les limites des maisons qui correspondent à cette définition. Autrement dit, un astre quelconque demeure le même temps, 1/6 de sa durée de visibilité, dans chacune des six maisons diurnes (12, 11, 10, 9, 8. 7) et 1/6 de la durée de son coucher dans les maisons nocturnes (6, 5, 4, 3, 2, 1). Mais le séjour dans chaque maison diurne (D/6) est en général très différent du séjour dans chaque maison nocturne (N/6) : cette différence est uniquement fonction du 8 de l'astre considéré (formule 1). Seuls les astres qui décrivent l'équateur passent deux heures dans toutes les maisons diurnes ou nocturnes : chaque maison contient 30° d'équateur.
La position des pointes (intersections de l'écliptique et des limites des maisons) découle de la définition ci-dessus et du temps sidéral considéré. Il est assez facile de la calculer. Mais il existe des tables qui, pour diverses latitudes rondes q> et pour toutes les valeurs du temps sidéral (de quatre en quatre minutes par exemple) fournissent les positions des pointes. Il ne reste qu'à interpoler doublement (pour la latitude exacte et pour l'heure exacte).
Le nombre moyen des réussites est np (moyenne).
Si l'événement survient x fois,le nombre algébrique h = x - np s'appelle l'écart. Le nombre u = v2npq s'appelle unité d'écart.
La probabilité pour qu'un écart h observé dépasse, en valeur absolue, u, puis 2 u, 3 u, 4 u est donnée par le tableau suivant:
Donc il y a seize chances sur cent cas pour qu'on observe un écart (en plus ou en moins par rapport à la moyenne) supérieur à u
5 chances sur 1.000 pour que l'écart dépasse 2 u
2 chances sur 10.000 pour que l'écart dépasse 3 u
15 chances 1 milliard pour que l'écart dépasse 4 u
Autrement dit, les grands écarts (par rapport à u) deviennent vite invraisemblables, impossibles à attribuer au hasard pur. Mais inversement, il n'y a lieu de chercher une cause, autre que le hasard, que si l'écart est grand par rapport à u.
Exemple. - On joue à pile ou face. Dans ce cas: p = 1/2, q = 1/2
1er cas. - Pour une partie de deux cents coups, la moyenne est cent et u = 10.
La plupart des parties de deux cents coups auront un résultat (face, par exemple) compris entre quatre-vingt-dix et cent dix. Cependant, il ne sera pas étonnant qu'un résultat déborde ces limites, en direction de quatre-vingts ou de cent vingt, car cela arrivera encore seize fois sur cent parties (résultats normaux).
Un résultat entre 70 et 80 (ou entre 120 et 130), serait déjà rare. En jouant une partie chaque jour, cela n'arrivera guère qu'une fois par an.
Mais un résultat dépassant 130 ou inférieur à 70 serait exceptionnel (une fois en trente ans).
Quant à un résultat dépassant 149 ou inférleur à 60, il faudrait vivre plus de cent mille ans en jouant chaque jour une partie, pour espérer le voir survenir.
Un seul résultat de cette nature rend le truquage de la pièce certain (pièce plombée d'un côté).
Autrement dit, certains résultats s'expliquent par le hasard seul; d'autres, au contraire, suggèrent le besoin d'une explication différente: leur caractère n'est plus fortuit; il devient systématique.
Résumons cette discussion des résultats Face, par exemple, des parties de 200 coups.

exc. - résultats exceptionnels; Invr. - résultats invraisemblables
Les pourcentages des résultats normaux ont été arrondis (les fréquences minimes des autres colonnes étant négligées).
2e cas. - Considérons maintenant une partie de vingt mille coups. Moyenne 10.000 et u = 100.
Voici la fréquence avec laquelle le résultat d'une partie tomberait entre les limites suivantes:

exc. exceptionnels; invr. invraisemblables
En comparant les écarts exceptionnels et invraisemblables du cas n° 2 à ceux du cas n° 1, on s'aperçoit qu'ils sont devenus seulement dix fois plus grands (300 au lieu de 30, 400 au lieu de 40) alors que le nombre des parties est devenu cent fois plus grand.
Cela montre le danger d'une statistique trop courte:
Cas n° 1 (deux cents parties) : les écarts atteignant 30 à 40 % de la valeur moyenne peuvent encore se rencontrer;
Cas n° 2 (vingt mille parties) : les écarts dépassant 4 % de la valeur moyenne sont « impossibles ».
jusqu'au point de marquer dans les cieux notre sort:Le régime d'heure d'été étant en vigueur, et Paris appartenant au fuseau zéro, l'heure T. U. de l'événement est 12 h. 52 min.
Le 1er août 1951, à 0 heure T. U., l'heure sidérale est 20 h. 35 min. 11 sec. (donnée prise dans un annuaire). L' événement a lieu 12 h. 52 min. de T. U. plus tard, c'est-à-dire 12 h. 54 min. 7 sec. de temps sidéral plus tard. (L'addition de 2 min. 7 sec. tient compte de la différence entre temps solaire et temps sidéral: nous avons signalé l'écart quotidien de quatre minutes environ.) .
Cela étant, l'événemènt s'est produit à 20 h. 35 min. Il sec. + 12 h. 54 min. 7 sec. = 9 h. 29 min. 18 sec. en temps sidéral de Greenwich (24 h. ayant été retranchées).
Comme Paris se trouve à 9 min. 21 sec. de longitude à l'Est du méridien de Greenwich, l'heure sidérale locale de l'événement, que nous cherchons est, finalement, 9 h. 38 min. 39 sec.
On voit que ce calcul fait intervenir la longitude du lieu et la connaissance de l'heure sidérale à 0 heure T. U. au jour considéré.
En réalité, si l'on considère comme négligeable une erreur de plusieurs minutes, on peut abréger notablement l'opération.
Tout d'abord l'heure sidérale à 0 heure T. U. est toujours à peu près la même à une date donnée. Sa valeur passe de 0 heure à l'équinoxe d'automne (vers le 23 septembre) à 12 heures pour l'équinoxe de printemps et à 24 heures (0 heure) pour l'équinoxe d'automne suivant, croissant d'environ 3 min. 57 sec. par jour. Seules les discontinuités de notre calendrier et les incommensurabilités des périodes célestes entre elles introduisent un écart annuel qui peut ne pas dépasser ± 2 minutes. A cet écart près on peut donc se servir d'une petite table perpétuelle au lieu d'un annuaire.
D'autre part, la conversion de l'heure T. U. de l'événement en temps sidéral peut être négligée puisque la correction peut ne pas dépasser non plus ± 2 minutes (d'où la règle).
II. - Table des valeurs approchées du temps sidéral à 0 heure de dix en dix jours
T | T | T | T | ||||||||
| 1er janvier | 6h.40 | 11 avril | 13h.14 | 20 juillet | 19h.49 | 28 octobre | 2h.23 | ||||
| 11 janvier | 7h.19 | 21 avril | 13h.54 | 30 juillet | 20h.28 | 7 novembre | 3h.02 | ||||
| 21 janvier | 7h.59 | 1er mai | 14h.33 | 9 août | 21 h. 07 | 17 novembre | 19h.09 | ||||
| 31 janvier | 8h.38 | 11 mai | 15h.13 | 19 août | 21 h. 47 | 27 novembre | 19h.09 | ||||
| 10 février | 9h.18 | 21 mai | 15h.52 | 29 août | 22 h. 26 | 7 décembre | 5h.00 | ||||
| 20 février | 9h.57 | 31 mai | 16h.31 | 8 septembre | 23h.06 | 17 décembre | 5h.40 | ||||
| 2 mars | 10h.37 | 10 juin | 17h.11 | 18 septembre | 13h.45 | 27 décembre | 6h.19 | ||||
| 12 mars | 11h.16 | 20 juin | 17h.50 | 28 septembre | 0h.25 | (6 janvier) | 6h.59 | ||||
| 22 mars | 11h.55 | 30 juin | 18h.30 | 8 octobre | 1h.04 | ||||||
| 1er avril | 12h.35 | 10 juillet | 19h.09 | 18 octobre | 1h.43 |
III. - Maisons
Le mouvement diurne fait décrire à tout astre un parallèle céleste suffisamment défini par sa déclinaison 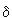 .
.
En un lieu de latitude connue 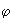 , si l'horizon coupe ce petit cercle, l'astre se lève et se couche: un arc D de sa trajectoire est diurne, le reste N est invisible en ce lieu (arc nocturne). On peut calculer l'arc D en degrés, et par suite la durée de la visibilité de l'astre, par la formule
, si l'horizon coupe ce petit cercle, l'astre se lève et se couche: un arc D de sa trajectoire est diurne, le reste N est invisible en ce lieu (arc nocturne). On peut calculer l'arc D en degrés, et par suite la durée de la visibilité de l'astre, par la formule
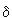 tg
tg 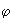
La définition classique des maisons, suivant Ptolémée, est la suivante:
« Chaque maison contient D/6 ou N/6 selon qu'elle est diurne ou nocturne.»
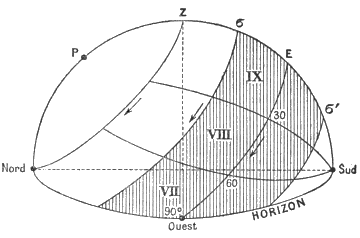 Fig. 14 |
La figure (14) montre les limites des maisons qui correspondent à cette définition. Autrement dit, un astre quelconque demeure le même temps, 1/6 de sa durée de visibilité, dans chacune des six maisons diurnes (12, 11, 10, 9, 8. 7) et 1/6 de la durée de son coucher dans les maisons nocturnes (6, 5, 4, 3, 2, 1). Mais le séjour dans chaque maison diurne (D/6) est en général très différent du séjour dans chaque maison nocturne (N/6) : cette différence est uniquement fonction du 8 de l'astre considéré (formule 1). Seuls les astres qui décrivent l'équateur passent deux heures dans toutes les maisons diurnes ou nocturnes : chaque maison contient 30° d'équateur.
La position des pointes (intersections de l'écliptique et des limites des maisons) découle de la définition ci-dessus et du temps sidéral considéré. Il est assez facile de la calculer. Mais il existe des tables qui, pour diverses latitudes rondes q> et pour toutes les valeurs du temps sidéral (de quatre en quatre minutes par exemple) fournissent les positions des pointes. Il ne reste qu'à interpoler doublement (pour la latitude exacte et pour l'heure exacte).
IV. - Sur la vraisemblance de certains écarts
Considérons n épreuves, où la réussite d'un événement ait à chaque fois pour probabilité p (p, pourcentage, nombre compris entre 0 et 1). Posons q = 1 - p.Le nombre moyen des réussites est np (moyenne).
Si l'événement survient x fois,le nombre algébrique h = x - np s'appelle l'écart. Le nombre u = v2npq s'appelle unité d'écart.
La probabilité pour qu'un écart h observé dépasse, en valeur absolue, u, puis 2 u, 3 u, 4 u est donnée par le tableau suivant:
| |h| | Probabilité de dépassement |
| u | 0,16 |
| 2 u | 0,005 |
| 3 u | 0,0002 |
| 4 u | 0,000.000.015 |
Donc il y a seize chances sur cent cas pour qu'on observe un écart (en plus ou en moins par rapport à la moyenne) supérieur à u
5 chances sur 1.000 pour que l'écart dépasse 2 u
2 chances sur 10.000 pour que l'écart dépasse 3 u
15 chances 1 milliard pour que l'écart dépasse 4 u
Autrement dit, les grands écarts (par rapport à u) deviennent vite invraisemblables, impossibles à attribuer au hasard pur. Mais inversement, il n'y a lieu de chercher une cause, autre que le hasard, que si l'écart est grand par rapport à u.
Exemple. - On joue à pile ou face. Dans ce cas: p = 1/2, q = 1/2
1er cas. - Pour une partie de deux cents coups, la moyenne est cent et u = 10.
La plupart des parties de deux cents coups auront un résultat (face, par exemple) compris entre quatre-vingt-dix et cent dix. Cependant, il ne sera pas étonnant qu'un résultat déborde ces limites, en direction de quatre-vingts ou de cent vingt, car cela arrivera encore seize fois sur cent parties (résultats normaux).
Un résultat entre 70 et 80 (ou entre 120 et 130), serait déjà rare. En jouant une partie chaque jour, cela n'arrivera guère qu'une fois par an.
Mais un résultat dépassant 130 ou inférieur à 70 serait exceptionnel (une fois en trente ans).
Quant à un résultat dépassant 149 ou inférleur à 60, il faudrait vivre plus de cent mille ans en jouant chaque jour une partie, pour espérer le voir survenir.
Un seul résultat de cette nature rend le truquage de la pièce certain (pièce plombée d'un côté).
Autrement dit, certains résultats s'expliquent par le hasard seul; d'autres, au contraire, suggèrent le besoin d'une explication différente: leur caractère n'est plus fortuit; il devient systématique.
Résumons cette discussion des résultats Face, par exemple, des parties de 200 coups.

exc. - résultats exceptionnels; Invr. - résultats invraisemblables
2e cas. - Considérons maintenant une partie de vingt mille coups. Moyenne 10.000 et u = 100.
Voici la fréquence avec laquelle le résultat d'une partie tomberait entre les limites suivantes:

exc. exceptionnels; invr. invraisemblables
En comparant les écarts exceptionnels et invraisemblables du cas n° 2 à ceux du cas n° 1, on s'aperçoit qu'ils sont devenus seulement dix fois plus grands (300 au lieu de 30, 400 au lieu de 40) alors que le nombre des parties est devenu cent fois plus grand.
Cela montre le danger d'une statistique trop courte:
Cas n° 1 (deux cents parties) : les écarts atteignant 30 à 40 % de la valeur moyenne peuvent encore se rencontrer;
Cas n° 2 (vingt mille parties) : les écarts dépassant 4 % de la valeur moyenne sont « impossibles ».
V. - Textes divers intéressant l'astrologie
ISAIE 47, versets 1, ..., 12, 13, 14
1) Descend.. et assieds-toi dans la poussière, vierge, reine de Babylone: tu n'as plus de trône, fille des Chaldéens.
. . . . . . . . . . . . . . . . . . . . . . . . . . .
12) Parais donc, avec tes enchantements, avec la multitude de ces sortilèges auxquels tu t'exerças dès ta jeunesse.
Peut-être pourras-tu en tirer profit.
Peut-être pourras-tu te rendre redoutable.
13) Tu t'es fatiguée à consulter tous les devins, qu'ils paraissent donc, ces astrologues, ces contemplateurs d'étoiles, ces pronostiqueurs à la Lune, et qu'ils te sauvent du malheur qui va fondre sur toi.
14) Les voici devenus comme du chaume; le feu va les consumer, ils ne préserveront pas leurs vies des atteintes de la flamme; ... ; nul ne pourra te sauver.
LA FONTAINE, L'horoscope (fable XVI, Liv. VIII)
. . . . . . . . . . . . . . . . . . . . . . . . . . .
Je ne vois point que la Nature
se soit lié les mains, et nous les lie encor
il dépend d'une conjoncture
de lieux, de personnes, de temps,
non des conjonctions de tous ces charlatans.
Ce berger et ce roi sont sous même planète;
l'un porte le sceptre, et l'autre la houlette:
Jupiter le voulait ainsi.
Qu'est-ce que Jupiter? un corps sans connaissance.
D'où vient donc que son influence
agit différemment sur ces deux hommes-ci?
. . . . . . . . . . . . . . . . . . . . . . . . . . .
L'ètat où nous voyons l'Europe
mérite que du moins quelqu'un d'eux l'ait prévu:
que ne l'a-t-il donc dit? Mais nul d'eux ne l'a su.
L'immense éloignement, le point et sa vitesse,
celle aussi de nos passions,
permettent-ils à leur faiblesse
de suivre pas à pas toutes nos actions?
Notre sort en dépend: sa course entre-suivie
ne va, non plus que nous, jamais d'un même pas ;
et ces gens veulent au compas
tracer le cours de notre vie!
Il ne se faut point arrêter
aux deux faits ambigus que je viens de conter.
Ce fils par trop chéri, ni le bonhomme Eschyle,
n'y font rien: tout aveugle et menteur qu'est cet art,
il peut frapper au but une fois entre mille;
ce sont des effets du hasard.
SAINT AUGUSTIN, Les confessions (Liv. IV, chap. III)
Augustin, en sa jeunesse, croit à l'astrologie et résiste aux premières tentatives faites pour désiller ses yeux.
Aussi je ne cessais pas de consulter Ces imposteurs qu'on nomme astrologues... (mathematicos).
La piété chrétienne, la piété véritable, repousse ces pratiques el les condamne... Souvenez.vous des paroles du Seigneur: « Voici que tu es guéri; ne pèche plus désormais, sinon crains le pire. » Ce précepte salutaire, les astrologues essaient de l'abolir, quand ils disent: « La cause inévitable du péché te vient du ciel» ou bien: « C'est Vénus, ou Saturne, ou
Mars, le responsable.» Ainsi ils acquittent l'homme de toute faute - l'homme de chair, de sang, d'orgueilleuse pourriture - et en chargent le créateur, l'ordonnateur du ciel et des astres...
J'eus l'occasion de dire à un homme de grand esprit, très habile médecin (Vindicianus), que je me plongeais dans des livres d'horoscopes; il m'invita avec une bienveillance paternelle à les rejeter, à ne pas gaspiller dans ces chimères du temps et du travail qui permettraient œuvre utile. Lui aussi avait, dans sa jeunesse, cultivé l'astrologie au point d'avoir songé à enfaire sa profession. Mais il en avait découvert l'absolue fausseté et n'avait pas voulu gagner sa vie en faisant des dupes.
Je lui demandai alors comment, à partir de telles erreurs, on peut prédire beaucoup de choses vraies. Il répondit qu'à son avis Îl la cause en était le hasard, fort répandu partout dans la nature. Consultez un poème quelconque chantant n'importe quoi dans une intention quelconque : vous y trouverez souvent un vers, au hasard, et sans qu'il y ait lieu de s'étonner, qui réponde à merveille à l'affaire qui vous occupe. De même, il arrive que l'esprit humain en vertu de quelque instinct supérieur et inconscient de ce qui se passe en lui, émette par hasard et non par l'effet d'un art, quelqe sentence qui convienne aux faits et gestes du questionneur.
. . . . . . . . . . . . . . . . . . . . . . . . . . .
Mais, à cette époque, ni ce médecin (Vindicianus), ni mon très cher ami Nébridius, qui se moquait de toute cette gent divinatoire, ne purent me persuader d'y renoncer. Ce qui m'impressionnait le plus, c'était l'autorité des auteurs qui en ont écrit; je n'avais pas encore trouvé de preuve évidente qui me fît voir clairement que les réussites des astrologues étaient l'œuvre du hasard, d'une rencontre, et non de l'art d'observer les astres.
Les confessions, Liv. VII, chap. VI
Augustin se libère de la croyance à l'astrologieC'est vous, vous seule, sagesse divine, ..., qui êtes venue à bout de l'entêtement que j'opposais au fin vieillard Vindicianus, Comme à l'adolescent Nébridius, à l'âme merveilleuse. Le premier affirmait avec véhémence, et le second ne cessait de me répéter, toutefois avec moins d'assurance, qu'il n'y a point d'art de prédire l'avenir, que les conjectures ont souvent l'appui du hasard, qu'à force de parler on finit bien par dire quelque vérité; il suffit de ne pas se taire pour tomber juste en quelque point.
C'est donc vous qui m'avez donné un ami, Firminus, qui connaissait mal l'astrologie mais aimait à consulter les astrologues, malgré certaine aventure dont son père lui avait parlé et qui était propre à ruiner sa croyance en l'astrologie...
Firminus tenait de son père l'anecdole suivante.
Au moment où la mère de Firminus le portait en elle, la servante d'un ami de la famille se trouvait grosse, elle aussi... Or il advint qu'elles accouchèrent toutes deux au même instant, de sorte qu'on dut tirer le même horoscope, jusque dans les moindres détails, et pour Firminus, et pour le petit esclave...
Et pourtant Firminus, fils de grande famille, courait les routes brillantes du siècle, voyait s'accroitre ses richesses, s'élevait aux plus hautes charges, tandis que l'esclave, sous un joug sans relâche, servait toujours ses maîtres.,.
Mes résistances fléchirent, puis tombèrent: je conclus que les horoscopes vrais procèdent du hasard et non d'un art, et que les horoscopes faux ne sont pas dus à l'ignorance d'un art mais à un mensonge du hasard.
Sorti de l'ornière, je ruminais des répliques à l'objection que pourrait me faire tel de ces fous qui pratiquent pareil métier et que désormais j'entendais attaquer: le récit de Firminus était-il sûr?
C'est alors que je réfléchis aux enfants qui naissent jumeaux. Le plus souvent, ils se suivent de si près que l'intervalle de leurs naissances, quelque importance qu'on prétende lui attribuer, est inappréciable et ne saurait se traduire par une différence dans les signes, sur lesquels l'astrologue fonde un horoscope vrai.
Ainsi l'astrologue aurait du prédire le même sort à Esaü et à Jacob, qui eurent des aventures bien dissemblables. Pour que ses prédictions fussent vraies, elles auraient du différer en dépit de l'identité des horoscopes. Il n'y a donc point d'art divinatoire. C'est par hasard, qu'on prédit vrai.