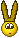La Terre trop petite sur une photo d'Apollo XVII?
Les photos du ciel du programme Apollo ont été abondamment critiquées parce qu'on n'y voyait pas d'étoiles. Voila qu'on prétend aussi que la Terre y apparait trop petite.

A gauche la photo AS17-134-20384, montrant l'astronaute Jack Schmitt à coté du drapeau, et la Terre visible au fond.
A droite ce qu'on prétend qu'aurait du être cette photo si la Terre avait paru avec sa taille normale.
Et bien sûr, cette taille trop petite prouve que ces photos on été prises en studio, par des photographes tenus au secret, mais qui avaient imaginé ce moyen de dévoiler l'imposture (ce que David Percy et Mary Bennett, appellent des "Whistle-blowers" (vendeurs de mèche).
(extrait d'une photo montrant la même scène sur le film 70 mm original, dont le scan fait 14160 pixels de large)
Mais non, il ne s'agit pas trouver une photo montrant la Terre la plus grosse possible, mais de savoir quel taille elle devrait avoir sur la photo.
L'auteur du montage "à la grosse Terre" n'a pas voulu faire de calculs géométriques, car, tout en prétendant bien s'y connaitre en géométrie et en perspective, il affirme péremptoirement que
"la taille d'un objet sur la photo n'est pas une fonction linéaire de sa distance à l'appareil."
Si!
Et il ajoute doctoralement:
Certaines personnes pensent qu'il est possible de déterminer directement la taille d'un objet sur la photo connaissant sa taille réelle et sa distance à l'appareil, mais c'est loin d'être aussi simple.
C'est vrai jusqu'à une certaine distance, mais plus la distance devient importante, et moins c'est vrai.
Hum! Il semble, bien que c'est le contraire qui est vrai: plus la distance est grande, plus la distance focale devient négligeable devant elle, et tous les manuels de trigonométrie enseigne que pour les petits angles, on peut confondre la tangente, et l'angle exprimé en radians. Mais l'auteur prétend prouver ce qu'il affirme par l'expérience.
Dans une première version de sa page, il employait une photo de chaises, puis, pour faire plus convaincant, une photo de la tour Eiffel, prise depuis la tour Montparnasse.
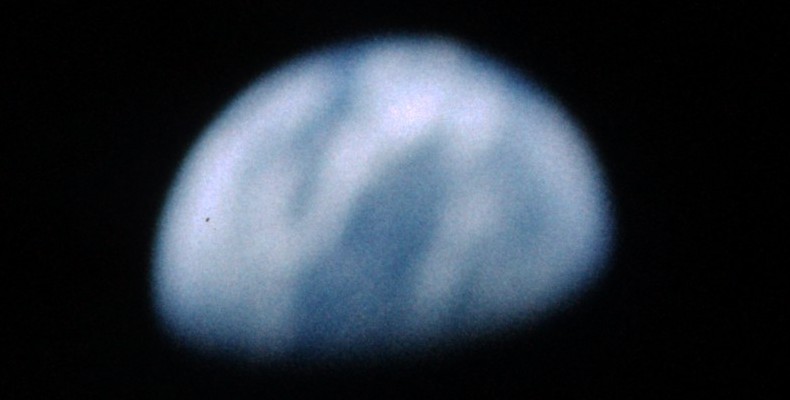
La preuve par la tour Eiffel.

A droite, La tour Eiffel serait, sur la photo, plus grande qu'elle ne devrait être, selon le calcul de l'auteur, qui a reconstitué sa "vraie taille". Peu lui chaut qu'elle n'atteigne pas l'horizon, et soit donc moins haute que la tour Montparnasse.
Enfin, dans une nouvelle version, il se rabat sur une photo montrant les deux tours, prise depuis la coupole du Sacré-coeur de Montmartre.
Ceci est une photo prise depuis le sacré-coeur avec un angle de vue large de 92,6°; j'ai pu le calculer parce que celui qui a pris cette photo a donné les caractéristiques de son appareil (distance focale de 17mm, largeur film de 14 pouces).
La photo a une largeur de 270mm sur l'écran, et la tour Eiffel une hauteur de 12mm, ce qui correspond dont à un angle de vue de 4,115° pour la tour Eiffel (l'image complète faisant 92,6°).
|
EN RÉALITÉ Il y a beaucoup d'erreurs dans cette description. La photo, qui a été prise par Bruno Monginoux, est effectivement disponible avec son exif, à cette adresse. Mais elle n'a pas été prise sur un film de 14 pouces, ce qui ferait 355.6 mm, mais avec un Nikon D50, dont le capteur fait 23,7 x 15,6 mm. La largeur de l'image sur l'écran ne fait rien à l'affaire, c'est sa taille en pixels qui est importante. Ici, elle est de 3008x2000, que l'auteur a réduit à 1024x680 sur sa page, et que nous avons réduit ici à 800x531. La distance focale indiquée dans l'exif est de 17 mm, ce qui nous ferait un champ de 69.76° et non 92.6°. Nous pouvons controler ce champ, grace aux positions sur l'image, et aux azimuts d'après Géoportails, de la tour Montparnasse et de la tour Eiffel. La médiane de l'image est à une abcisse de 1504 pixels. Nous cherchons alors l'azimut du centre de l'image pour que les tangentes des champs à droite et à gauche de la médiane, déduits des azimuts depuis le centre, soient identiques. De façon que: nous trouvons que l'azimut du centre est 211.79°, et que les 654 pixels d'abcisse relative de la tour Eiffel correspondent à une distance au centre de 5.153 mm et à un angle de 16.51°, dont la tangente est de 0.296. Ce qui nous permet de calculer que la focale réelle est de 17.4 mm, et donc le champ réel de 68.512°. |
La tour Eiffel a une hauteur de 320m et est à 4690m du sacré-coeur, d'où est prise la photo, avec l'angle de vue de 4,115°, cela donnerait une hauteur de 337 mètres pour la tour Eiffel, donc un peu plus grand que la hauteur réelle.
|
EN RÉALITÉ
Le sommet de la tour est à 296 pixels sous la médiane horizontale, soit 2.31 mm et celui de la voùte à 434 pixels, soit 3.38 mm sur le capteur. En oubliant la distorsion, cela nous fait 7.558° et 10.993°, soit 3.435° pour la partie visible et non 4.115°. Pour la hauteur, en prenant comme base la médiane horizontale, au niveau de la tour, le sommet est à 622 m sous la médiane, et l'arche à 912 m, ce qui nous fait une différence de 290 m, ce qui est compatible avec nos 286 m, vu la faible précision de la photo. |
La différence n'est pas énorme, mais pour des distances beaucoup plus importantes, l'écart entre l'angle réel et l'angle théorique devient plus conséquent.
Et pour la terre vue depuis la lune ou la lune depuis la terre, la distance est tellement énorme que la différence entre l'angle réel et l'angle théorique devient beaucoup plus impôrtant.
Donc, si la terre apparaît sous son angle théorique sur les photos d'Apollo, cela prouve au contraire qu'elle apparaît trop petite, car elle devrait apparaître plus grosse
Et, apparemment, il serait le seul à l'avoir compris, bien qu'il n'en donne aucune démonstration...

Comment, dès lors, retrouver la vraie taille apparente de la Terre vue de la lune? En mesurant la taille apparente de la lune vue de la Terre, puisque la distance est la même que celle de la Terre vue de la lune, et en la multipliant par le rapport des diamètres.
Certes, le principe n'est pas idiot, quoiqu'il ne soit valable que pour les petits angles, quand on peut confondre la tangente et l'angle exprimé en radians, et surtout qu'il faut compter la distance entre l'astre et l'appareil photo, et non la distance entre les centres des deux astres.
La preuve par l'appareil photo de bas de gamme.
 |
 |  |  |  |
A gauche, une photo de la lune presque pleine. Ensuite une photo de la Terre ajustée à la même taille que la lune. Puis la même photo respectant sa taille relative par rapport à la lune. Enfin une comparaison entre cette photo et celle que prévoient les lois de la géométrie
Et voila! L'auteur vient de vous démontrer que des deux photos montrées tout en haut, la bonne est celle de droite. Les astronomes, géomètres et autres photographes ont tout faux! un appareil photo de bas de gamme a suffi. Euclide doit s'en retourner dans sa tombe.
|
EN RÉALITÉ Devons nous vraiment croire que des photos prises, dans des conditions mal précisées, avec un appareil bas de gamme, jette à bas une science millénaire, vérifiée des milliards de fois? Sur le site de l'auteur, la photo est disponible avec son exif. En nous documentant sur l'appareil, nous apprenons que le Fujifilm Finepix A101, a une résolution de 1280*960, un zoom numérique 2x, une focale equivalente pour film 35mm de 36 mm, et que la taille de son capteur est de 5.312 x 3.984 mm. Alors là, il y a un os!
On remarque la présence de la Terre, mais plus encore le cadrage bizarre, du à ce que les Hasselblad lunaires n'avaient pas de viseur. A droite, nous avons rectifié l'orientation, et on voit,dans le reflet de la visière, que Gene Cernan s'est abaissé pour prendre la photo en contre plongée. Maintenant, pour trouver les dimensions apparentes des objets sur les photos d'Apollo, un détail nous aide: les photos prises au Hasselblad portaient l'amorce d'un carroyage, que nous avons exagéré ici, en traçant, en blanc, les croix sur le fond noir du ciel.
Les croix sont espacées de 10 mm sur le film, et la focale de l'objectif Biogon, 61.1 mm, nous permet de retrouver les angles. En travaillant sur l'image AS17-134-20384 de l'Apollo 17 Lunar Surface Journal, qui fait 2340 pixels de large, nous trouvons que les croix sont espacées de 454 pixels sur le scan et l'image de la Terre, assez floue s'inscrit dans un disque de 108 pixels de diamètre maximum, dont le centre à 741 pixels du centre du champ, ce qui correspond à 16.32 mm sur le film. Or nous connaissons parfaitement l'instant de prise de vue: 118 heures 25 minutes 54 secondes après le décollage qui eut lieu le 7 décembre 1972 à 5H 33 GMT: L'image a donc été prise le 12 décembre 1972 à 3H 58 mn GMT. Grace au logiciel Stellarium, nous connaissons la distance Terre-lune à cet instant: 393 119 km. Mais c'est la distance du centre de la Terre au centre de la lune. Il faut tenir compte de ce que la photo est prise depuis la surface de la lune, et de ce que la Terre n'est pas au zénith, mais à environ 20° au dessus de l'horizon, ce qui donne une distance de 392 525 Km. Prenant le diamètre moyen de la Terre augmenté d'une trentaine de km, pour tenir compte de l'épaisseur de l'atmosphère, cela donne 12760 km. nous pouvons en déduire le diamètre apparent de la Terre vue de l'emplacement de la mission Apollo 17: 1.8624°. Si l'image était au centre du champ, nous en déduirions immédiatement la dimension qu'elle devrait avoir sur le scan, en se basant sur la focale du Biogon: 2*tan(1.8624/2)*61.1*454/10 = 90 pixels.Voila qui est un peu fort! Alors qu'on accuse cette photo de montrer la Terre trop petite, nous découvront au contraire qu'elle montre une image de 108 pixels au mieu de 90, donc trop grosse! Mais rappelons nous l'énorme Terre montrée plus haut: elle parait un peu flou. Et rappelons nous aussi que Gene Cernan photographiait son compagnon de près: Il est donc logique qu'il ait tourné la bague de mise au point pour avoir une photo plus nette, quitte à avoir la Terre plus floue. L'objectif Biogon permettait une mise au point jusqu'à 0.90 m. Si Cernan avait tourné la bague à fond, il nous suffit d'appliquer la formule c*c' = f² pour trouver que la distance focale avait augmenté de 4.148 mm pour devenir 65.248 mm. C'est avec cette distance focale qu'il faut compter. Et voila! Pas besoin de réformer l'astronomie ou la géométrie. L'aspect de la Terre sur cette photo est parfaitement normal. Il est tout de même curieux que notre auteur puisse affirmer sans rougir que la taille apparente (ou du moins, sa tangente), n'est pas inversement proportionnelle à la distance. C'est aussi absurde que l'opinion des Athéniens, qui soutenaient contre Anaxagore que le Soleil n'avait qu'un pied de large. |
La preuve par le double décimètre.
L'auteur a trouvé une autre preuve de trucage: la taille de la Terre n'est pas la même sur les photos d'Apollo 11 et d'Apollo 17:
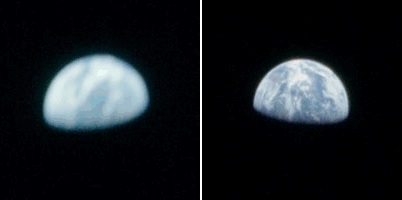
J'ai pris une fenêtre contenant la terre d'exactement la même taille sur les deux photos haute résolution (200x200 pixels); la terre devrait logiquement avoir la même taille sur les deux photos, et pourtant, vous pouvez constater ce n'est pas le cas; la terre d'Apollo 17 est légèrement plus grosse que celle d'Apollo 11; sur mon écran, j'ai mesuré 2,8cm pour le diamètre de la terre d'Apollo 17 (dans paint, sur la photo haute résolution), et 2,5cm pour la terre d'APollo 11; cela fait un rapport de 1,12 entre la terre d'Apollo 17 et celle d'Apollo 11 (cela pourrait même faire un peu plus, car la photos d'Apollo 11 est légèrement plus grande que celle d'Apollo 17). Donc, pour une distance égale de la terre, la terre d'Apollo 17 est 1,12 fois trop grosse relativement à celle d'Apollo 11.
|
EN RÉALITÉ Ce que tout le monde peut constater, c'est que si la Terre de la photo d'Apollo 17 parait plus grande que sur la photo d'Apollo 11, elle parait aussi plus floue. Et pour cause: la mise au point n'avait pas été faite sur l'infini, mais au minimum, pour être au point sur l'astronaute au premier plan. Nous avons vu que la Terre avait un diamètre apparent de 1.862°, que le décalage de la mise au point en avait fait une image de 108 pixels, et que c'était normal. Nous devrions décerner un bonnet d'âne pour notre complotiste. |
| Accueil | Paranormal | Espace | Moonhoax | Anomalies des photos |
| Dernière mise à jour: 28/12/2020 |