La "loi" de Titius-Bode
Les idées antiques
Ayant découvert que l'harmonie des notes de musique procédait de rapports simples entre nombres entiers, il étendit cette règle à l’Univers entier. Dans le système pythagoricien, les astres mobiles tournent autour de la terre sur des orbites circulaires, dont les rayons sont entre eux dans des rapports simples, ce qui met les orbites en harmonie musicale entre elles et avec la sphère des étoiles fixes: C'est la "musique des sphères". Cette idée de Pythagore, abandonnée par la Science depuis bien des siècles, a encore cours chez les ésotéristes, et autres amateurs de "vibrations" |
 Platon |
«Puis, ce tout, il l'a partagé en autant de portions qu'il convenait, chacune d'elles étant mêlée de Même, d'Autre et de cette [troisième] substance susdite. Il a commencé le partage ainsi qu'il suit. En premier lieu, il a séparé du mélange total une portion. Ensuite il a pris une seconde portion double de celle-là ; puis une troisième portion égale à une fois et demie la seconde et à trois fois la première ; une quatrième double de la seconde : une cinquième triple de la troisième ; une sixième égale à huit fois la première ; une septième égale à vingt-sept fois la première. Après cela, il a comblé les intervalles doubles et triples, détachant encore des portions du mélange primitif et les disposant entre ces parties-là, de telle sorte que, dans chaque intervalle, il y eût deux médiétés.»
On voit ainsi apparaitre la progression 1,2,3,4,9,8,27. Mais il n'est dit nulle part, que cette suite de nombres s'applique aux planètes, d'autant que du temps de Platon, on ne connaissait que cinq planètes, et qu'on ignorait leurs distances
La révolution Copernicienne
Les conceptions antiques du système solaire, modélisées par Ptolémée ne permettaient pas de connaitre les distances des planètes. On se contentait de les ranger par ordre de durée de révolution.
Les anciens n'avaient d'ailleurs aucune raison de soupçonner de grandes différences de distance, car les éclats des planètes sont du même ordre de grandeur. Ainsi à son plus grand éclat, Mercure est plus brillante que Saturne de 2 magnitudes seulement, alors qu'elle serait moins brillante de 10 magnitudes, si elle était à la même distance
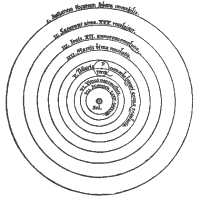 Système de Copernic |
Pourtant dans l'ouvrage de Copernic lui même, publié en 1543, rien ne distingue les distances des planètes entre elles de celles qu'imaginaient les anciens, car le schéma qu'il avait publié de son système ne respectait pas l'échelle des distances.
Énoncé au XVIème siècle, le système de Copernic ne s'imposa d'ailleurs qu'au siècle suivant
 Diamètres apparents (1 pixel = 1") |
C'est donc au XVIIème siècle, en calculant, et reproduisant à l'échelle, les rayons des orbites des planètes, qu'on se rendit compte que Jupiter et Saturne étaient beaucoup plus éloignés que Mars.

Distances au soleil des planètes visibles à l'oeil nu
Mais Pourquoi ce vide entre Jupiter et Mars? A l'époque, deux réponses étaient possibles. Ou ce vide existait vraiment, et avait une raison d'ètre, ou il n'existait pas vraiment, car il était occupé par un astre invisible.
 Jean Képler |
Cum igitur hac non succederet, alia via, mirum quam audaci, tentatavi aditum. Inter Jovem et Martem interposui novum planetam, itemque alium inter Venerem et Mercurium, quos duos forte ob exilitatem non videamus, iisque sua tempora periodika nscripsi. Sic enim existimabam, me aliquam aequalitatem proportionum effecturum, quae proportiones inter binos versus Solem ordine minuerentur, versus fixas augescerent: ut proprior est Terra Veneri in quantitate orbis Terrestris, quam Mars Terrae in quantitate orbis Martii. Verum neque unius planetae interpositio sufficiebat ingenti hiatui (signe jupiter) et (signe Mars). Manebat enim major Jovis ad illum novum proportio, quam est Saturni ad Jovem
Comme cela ne réusissait pas de cette façon, j'en tenté une approche par une autre voie, plus étonnante que hardie. Entre Mars et Jupiter j'ai intercalé une nouvelle planète, et de même une autre en Vénus et Mercure, que toutes deux, par hasard, nous n'apercevons pas à cause de leur petitesse, et je leur ai assigné des périodes (de révolution). Car j'estimais ainsi que je produirais quelque relation de proportion, qui diminuerait les rapports entre les paires du coté du soleil, et les augmenterait du coté des étoiles fixes: car plus spécifiquement de la Terre à Vénus en proportion de l'orbe terrestre, que de Mars à la Terre en proportion de l'orbe martienne. Pourtant une seule planète ne suffisait pas pour l'énorme vide Jupiter - Mars. Car il subsistait un plus grand rapport de Jupiter à la nouvelle, que de Saturne à Jupiter
Les polyèdres de Kepler
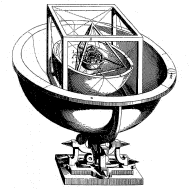 (cliquez pour agrandir) |
Dans ce système, qui ne fut d'ailleurs jamais utilisé, les orbites planétaires sont inscrites sur des sphères, lesquelles sont inscrites et exinscrites dans des polyèdres réguliers
En profitant de ce qu'il y a ainsi beaucoup de place vide entre les sphères inscrites et exinscrites au tétraèdre, Képler rendait à peu près compte du vide entre la sphère portant l'orbite de Mars, et celle portant l'orbite de Jupiter
C'était un peu rajouter des polyèdres de cristal, aux "cieux de cristal" d'Aristote. Heureusement, Képler vérifiait tout par le calcul, et finit par abandonner au musée des curiosités cette hypothèse qui ne marchait pas mieux que la précédente, et ne pouvait rendre compte des singularités de l'orbite de Mars
Galilée ayant découvert 4 satellites de Jupiter, le même Képler en profita pour imaginer une loi de répartition des satellites pour les planètes: 1 pour la Terre, 2 pour Mars, 4 pour Jupiter, 8 Pour Saturne (On remarque, que cette progression géométrique exclut la possibilité d'une planète entre Mars et Jupiter)
Cette idée l'induisit en erreur quand Galilée, pour prendre date, lui fit part de sa dernière découverte dans un message crypté par transposition:
Smaismrmilmepoetaleumibunenugttaviras
Sans attendre la confirmation, Képler tenta de reconstituer l'anagramme, et obtintSalve umbistineum geminatum Martia proles
Car bien entendu, le message était en latin.
Ce déchiffrement (au prix d'un latin pas très catholique), signifiait à peu près "Salut brulants jumeaux de Mars". Képler crut donc Que Galilée venait de découvrir ces deux lunes qu'il supposait à Mars. Hélas, le message original était:
Altissimum planetam tergeminum observavi
Galilée venait de découvrir deux appendices à Saturne (les anses des anneaux)
Cette erreur de Képler procède d'un curieux syndrome ou la réalité porte son propre masque. L'hypothèse de Képler sera reprise par Swift, dans "les voyages de Gulliver", puis par Voltaire dans "Micromégas", avant d'être confirmée par la découverte de Phobos et Deimos par Asaph Hall en 1877
Notons qu'en dehors des audaces de Képler, l'idée de planètes encore inconnues, fera son chemin, et réapparaitra au XVIIIème siècle, sous la plume de William Whiston ( successeur de Newton à Cambridge), en 1717, de Thomas Wright en 1742, ou de Clairaut en 1758. Le relativisme étant à la mode
L'autre solution, la réalité d'un vide, trouvera une justification avec la gravitation universelle. Newton, suivi plus tard par Kant et Lambert, remarque que du fait de la gravitation de Jupiter, ce vide est indispensable à la stabilité du système solaire.
Retenons qu'on imagina une loi arithmétique de répartition du nombre des satellites avant d'en imaginer une pour les distances des planètes
L'approche d'une loi
 James Gregory |
 Christian Wolff |
Cette progression de Gregory sera également citée en 1724, par le philosophe Christian Wolff, ce qui lui vaudra d'ètre parfois cité comme initiateur de la loi de Titius-Bode. Pire, on le confond parfois avec l'astronome Max Wolf, initiateur de la recherche photographique des petites planètes
En réalité, ni Gregory, ni Christian Wolf n'avaient mentionné de relation dans les chiffres qu'ils citaient, mais on pouvait remarquer qu'à condition de tenir compte d'une lacune entre Mars et Jupiter, les rayons des orbites des planètes suivent approximativement une loi géométrique. La distance au soleil semble doubler quand on passe d'une planète à la suivante (surtout pour les dernières).
La relation de Titius
 Titius |
Notez les distances des planètes de l'une à l'autre, et remarquez que presque toutes sont séparés les unes des autres dans une proportion qui s'accorde à leurs grandeurs corporelles. Divisez la distance du soleil à Saturne en 100 parts ; alors Mercure est séparé du soleil par quatre parts, Venus par 4+3=7 parts, la terre par 4+6=10, Mars par 4+12=16. Mais notez que cela de Mars à Jupiter il y a une déviation de cette si exacte progression. De Mars il y a un espace de 4+24=28 parts, mais jusqu'ici aucune planète n'y a été aperçue. Mais le Seigneur Architecte devrait-il avoir laissé cet espace vide ? Pas du tout. Supposons donc que cet espace appartient sans doute aux satellites non découverts encore de Mars, ajoutons aussi que peut-être, Jupiter en a autour de lui de plus petits qui n'ont pas encore été aperçu au télescope. À côté de cet espace encore inexploré par nous apparait la sphère d'influence de Jupiter à 4+48=52 parts; et celle de Saturne à 4+96=100 parts. Quelle relation merveilleuse !
En 1772, dans une deuxième édition, Titius publie cette fois cette remarque dans une note de bas de page. Bien qu'il ne donne pas de formule, on remarque bien la progression 3, 6, 12, 24, 48 ,96 (on remarque aussi qu'il a une notion très... très élastique de ce qu'est un satellite).
Cette note tombe alors sous les yeux du jeune Johann Elert Bode (il n'a que 25 ans), qui est en train de mettre la dernière main à son livre, Deutliche Anleitung zur Kenntniß des gestirnten Himmels (guide précis pour la connaissance du ciel étoilé).
 frontispice |
 Johann Elert Bode |
Dies letztere scheint insbesondere ans dem ganz bewundernswürdigen Verhältniß zu folgen, welches die bekannten sechs Hauptplaneten in ihrer Entfernung von der Sonne beobachten. Man nenne den Abstand des Saturns von der Sonne 100, so ist der Merkurius 4 solcher Theile von der Sonne entfernt. Die Venus 4 und 3 = 7. Die Erde 4 und 6 = 10. Der Mars 4 und 12 = 16. Nun aber kommt eine Lücke von dieser so ordentlichen Progreßion. Vom Mars an folgt ein Raum von 4 und 24 = 28 Theilen, worin bis jetz und noch kein Planet gesehen wird. Sollte der Urheber der Welt diesen Raum leer gelassen haben? dies ist nicht wahrscheinlich. Von hier kommen wir zu der Entfernung des Jupiters durch 4 und 48 = 52, und endlich des Sarurns durch 4 und 96 = 100 Theile.
Ce dernier point semble en particulier découler de la relation étonnante que les six planètes connues observent dans leurs distances du soleil. Prenons 100 pour la distance du soleil à Saturne, alors Mercure en est séparé par 4, Venus est à 4+3=7, La Terre 4+6=10, Mars 4+12=16. Vient maintenant une lacune dans cette progression si bien ordonnée. Après Mars suit un espace à 4+24=28, dans lesquelles aucune planète n'a été encore vue. Peut-on croire que le fondateur de l'univers avait laissé cet espace vide ? Ce n'est pas vraisemblable. D'ici nous arrivons à la distance de Jupiter à 4+48=52, et finalement à celle de Saturne à 4+96=100 parts.
L'ouvrage de Bode est publié en 1772. Bode qui recopie Titius, sans le mentionner, mais sans l'erreur des satellites, ne donne toujours pas de formule. Mais elle est implicite: A partir d'une progression géométrique de raison 2, on multiplie par 3 et on ajoute 4.
Plus tard on présentera cette relation en prenant la distance terre-soleil comme unité, c'est à dire en divisant chaque terme par 10. En partant de 0, on obtient:
|
Planète Mercure Vénus Terre Mars ... Jupiter Saturne |
"loi" .4 .7 1 1.6 2.8 5.2 10 |
Distance .387 .723 1 1.523 5.202 9.554 |
Sur le coup, cette correspondance, qui n'est que partielle, est considérée comme une simple curiosité
Tout va changer en 1781. William Herschel découvre un astre nouveau qu'il prend d'abord pour une comète, et qui s'avère finalement suivre une orbite de planète. Cette planète est baptisé Uranus. Une fois calculés les éléments de son orbite, on trouva que cette planète se trouvait à 19.2 unités astronomiques, alors qu'en prolongeant la loi de Titius Bode, on trouve 19.6.
La "curiosité" changeait de statut et devenait une loi prédictive.
Mais alors, si c'était une vraie loi, il devait exister réellement une planète, non encore découverte, correspondant à la valeur 2.8, où existait une lacune
En 1786 Jérome de Lalande propose une recherche systématique de la planète manquante.
A la recherche de la planète manquante
 Von Zach |
 le duc Ernst |
Non moins convaincu que Bode, il entreprit donc dès 1787 une recherche systématique en se limitant à la bande zodiacale.
En 1799, Von Zach n'ayant toujours rien trouvé, partit visiter d'autres astronomes à Breme, Celle et Lilienthal, et y trouva l'iidée d'une coopération astronomique internationale.
Le 21 Septembre 1800, Franz Xaver Von Zach, Johann Hieronymus Schröter, Heinrich Wilhelm Olbers, Carl Ludwig Harding , F.A. Freiherr von Ende et Johann Gildemeisterse se réunirent à Lilienthal et y élaborèrent un plan de bataille, où 24 astronomes se partageraient 24 zones zodiacales de 15 ° chacune, et en établiraient une carte précise qu'ils vérifieraient régulièrement afin d'ètre sûrs d'y détecter un astre intrus.
 Hegel |
Il partait, en effet, de la série de nombres donnée par Platon (en oubliant qu'il ne connaissait que 5 planètes), y remplaçait 8 par 16 sans autre forme de procès, et finalement retransformait le tout par une formule du type de la loi de Bode.
La "loi de Hegel" évacuait ainsi la facheuse lacune, mais avec ce genre de méthode, Hégel aurait aussi bien pu démontrer que la Terre n'avait pas de satellite...
Le Duc Ernst von Gotha, envoya à Von Zach un exemplaire de la thèse avec cette mention: "Monumentum insaniae saeculi decimi noni" ( monument à la folie du XIXème siècle )
Aujourd'hui, les disciples d'Hegel préfèrent jeter un voile pudique sur cet épisode de la vie de leur maitre

 Piazzi |
Le 1er janvier 1801, donc "lors de la première nuit du XIXème siècle", à Palerme, le père Giuseppe Piazzi, qui travaillait à établir un catalogue d'étoiles, découvre un nouvel astre dans la constellation du Taureau. Cet astre n'ayant ni coma, ni queue, Piazzi qui avait d'abord pensé ( comme Herschel ) à une comète, comprend qu'il peut s'agir d'une planète.
Malheureusement, dès le 11 février la planète se perd dans la lumière de l'astre du jour. Elle n'a été suivie que sur un arc de 9°. Pour la retrouver, il faut calculer son orbite, donc en déterminer les 6 éléments, et Piazzi dispose bien de 24 positions, mais parfois incertaines.
A cette époque on ne sait pas encore résoudre un système à 6 inconnues avec un nombre supérieur d'équations. Piazzi passe la main à Barnaba Oriani, Bode et Lalande
C'est alors que le jeune Karl Friedrich Gauss (il n'a que 24 ans) découvre le problème. Il développe de nouvelles méthodes de calcul, publie les positions prévues et le 7 décembre (d'autres disent le 31) Von Zach retrouve la planète. Le rayon de l'orbite est de 2.766 U.A.
Triomphe de la loi de Bode
Piazzi baptise la planète du nom de Cerere Ferdinandea, du nom de Cérès, divinité tutélaire de la Sicile, et de son roi, Ferdinand des deux Siciles. La loi de Bode triomphe (Titius était mort en 1796). Celle de Hegel disparait piteusement dans les oubliettes
 Olbers |
Et puis le 1 septembre 1804, Karl Ludwig Harding, autre membre de l'équipe, découvre Junon
Enfin le 29 mars 1807 Olbers découvre Vesta.
Tous ces petits astres gravitent entre Mars et Jupiter
Voilà qui est ennuyeux, car là où la loi de Bode prévoyait une planète, on en a trouvé quatre!
Mais l'orbite de ces 4 petites planètes avait un air de famille. Elles s'approchaient toutes d'un même point. Olbers en déduisit qu'elles étaient les fragments d'une planète plus grosse qui avait explosé. La loi de Bode l'avait échappé belle!
Johann Elert Bode, devenu directeur de l'observatoire de Berlin, mourut le 23 novembre 1826, sans avoir vu sa "loi" réfutée
Nouveau test pour la loi de Bode
Uranus, qui avait si bien validé la "loi", était rétive à respecter la mécanique céleste, avançant ou retardant d'une valeur bien supérieure aux erreurs d'observations
Quid? Alexis Bouvard, qui avait rédigé les tables de positions d'Uranus, expliqua que les perturbations d'Uranus devaient être causées par une planète encore inconnue
On se mit à calculer. Flemming, Adams et Leverrier calculèrent chacun de leur côté. Adams trouva le premier une orbite compatible avec les observations, mais ne réussit pas à initier la recherche visuelle de la planète.
Leverrier, avec une méthode plus compliquée trouva lui aussi les paramètres de la nouvelle planète, mais ne réussit pas mieux à lancer une recherche à Paris. C'est Galle, son correspondant de Berlin, qui découvrit la planète inconnue.
(voir: La découverte de Neptune
Le calcul triomphe!
Mais...la loi de Bode? Est elle confirmée encore une fois?
Feu la loi de Bode
Hé non! Cette fois ci, la loi de Bode n'est pas vérifiée. Pour simplifier leurs calculs Adams et Le Verrier avaient tous les deux pris la distance donnée par la loi de Bode comme base de départ, quitte à la réduire pour améliorer l'accord. Mais dès que d'autres observations eurent permis de calculer l'orbite réelle de la nouvelle planète on s'aperçut que cette orbite avait un rayon de 30.1 U.A. Donc- L'orbite calculée si laborieusement par Leverrier était fausse, le rayon calculé étant de 36.15 U.A
- L'orbite calculée par Adams, ne l'était pas moins: 37.25 U.A
- La loi de Bode échouait, puisqu'elle prévoyait 38.8 U.A
Ce n'est pas tout. Dès 1845 Hencke ( à ne pas confondre avec Encke) découvrait un nouvel astéroïde: Astrée. La chasse aux petites planètes recommençait, et le nombre de planètes trouvées (sans que la masse totale estimée atteigne celle de la lune) finit par invalider complètement l'hypothèse de la planète éclatée d'Olbers.
Neuf planètes au total ( en comptant Cérès ). Six déja connues. Trois prédictions. Une fausse réussite, un échec. C'est fini pour la loi de Bode, qu'on n'osera plus ressortir pour la découverte de Pluton ( 39.44 u.a. au lieu des 77.2 prévus par la loi ) On écrit parfois que cette "loi", était fausse, mais fut utile. Ce n'est même pas vrai au niveau théorique, puisqu'on n'avait pas attendu sa publication, pour imaginer des planètes encore à découvrir, et que les deux découvertes de planètes qui la vérifiait furent faites par hasard. Herschel et Piazzi pointaient des étoiles quand ils découvrirent Uranus et Cérès.
C'est même plutôt l'inverse car la loi de Bode induisit en erreur Adams et Leverrier qui calculèrent pour Neptune une orbite fausse, en sorte que si la recherche n'avait pu avoir lieu que des années après l'époque des calculs, on aurait pu rater la découverte de Neptune. Consolons nous en pensant qu'elle aurait inmanquablement été trouvée à la fin du XIXème siècle grace à la méthode de recherche photographique instaurée pour les petites planètes
Il y eut néanmoins une utilité à cette fausse loi, c'est la coopération internationale qu'elle initia pour la recherche de la planète manquante, et qui déboucha sur la création de périodiques spécifiquement consacrés à l'astronomie
De plus la "loi de Bode", qui devrait s'appeler "relation de Titius", est couramment présentée sous une formulation fausse:
d = .4 + .3 * 2 n
Or cette formule fonctionne de n = 0 ( Vénus ) à n = 5 ( Uranus ), mais est incapable de donner un résultat pour Mercure, à moins de partir de n = -1, et d'accepter de trouver d = .55 (au lieu de .387).

Les avatars de la loi de Bode
Après la loi de Hégel, la loi de Titius-Bode part donc au cimétière. Mais l'échec n'a pas découragé les chercheurs de Loi
 Babinet |
Nullement découragé, Babinet remit sa planète sur le tapis lors de la séance du 18 septembre, en indiquant sa position, mais toujours sans se baser sur aucun calcul. Le Verrier, toujours à son poste, n'eut aucune peine à lui faire remballer sa fameuse planète. La "loi de Babinet" n'aura vécu qu'un mois, mais ce fut suffisant pour qu'on trouve la trace de la planète de Babinet dans certains manuels de vulgarisation de l'époque.
Quand au nom, il fut donné au huitième Satellite de Saturne que Bond et Lassel venait de découvrir
Remarquons qu'à cette époque, On savait qu'un nuage de petites planètes remplissait la lacune de la loi de Bode, sans parvenir à atteindre la masse d'une honnète planète, ce qui mettait en lumière une autre lacune, théorique cette fois. La loi de Bode prétendait prédire les distances, mais pas les masses. Or Physiquement parlant, un astéroïde comme Cérès ne saurait prétendre à ètre une planète, au même titre que son voisin Jupiter, dix millions de fois plus gros!
 Kirkwood |
Ce travail lui valut d'être surnommé "le Képler américain" (...par les américains, of course)
Malheureusement, la "loi de Kirkwood" prévoyait une planète importante entre Mars et Jupiter...
Un coup d'oeil sur le diagramme ci dessous , montrant les planètes à l'échelle montre tout de suite deux types de planètes:
- Les planètes "telluriques", dont les tailles croissent, puis décroissent avec la distance, pour se perdre dans le nuage des astéroïdes
- Les planètes "joviennes", beaucoup plus grosses, et à la composition manifestement différente.
 Les planètes du système solaire (cliquez pour agrandir) |
Or Kirkwood n'avait tenu compte que d'une seule population de planètes. Sa loi est allé rejoindre celle de Hégel, de Bode et de Babinet au cimetière.
Heureusement, Daniel Kirkwood fut mieux inspiré en s'intéressant aux "résonances" des orbites. Il expliqua en 1866 que, dans les anneaux de Saturne, la division de Cassini était en résonance avec le satellite Encelade.
Encore raté pour la résonance des divisions des anneaux avec les satellites de Saturne, que les observations modernes ont infirmé.
Mais Kirkwood étendit sa découverte à la ceinture d'astéroïdes, en expliquant le mécanisme de formation de lacunes, en résonance avec Jupiter. Cette fois, les observations ultérieures confirmèrent sa théorie, et ces lacunes portent aujourd'hui son nom
Et les chercheurs modernes continuent. On peut citer la loi de Savart, basée sur le nombre d'or
La loi de Damiani
d = e(.422*n)[.36*SIN(9°*(n-.5))+.08*sin(49.5°*(n-.5))]
qui donne un meilleur résultat que la loi de Bode, mais utilise beaucoup de paramètres
La loi de Souriau, qu'il appelle loi dorée
d = ( (1/oméga)4/3)n , soit 1.9n
Simple n'est ce pas? Mais ça marche mieux avec 1.77n
La loi de Zartarian, basée sur la suite de Fibonaci, mais qui donne une relation pour les périodes, et non plus pour les distances. Il faut dire que l'auteur opère une savante salade, digne de Hégel, en mélangeant les périodes de révolution des planètes, de la lune, de rotation du soleil, et corrige l'erreur de Neptune et Pluton en faisant la moyenne des deux périodes! Même Képler n'aurait jamais osé...
Et enfin l'imbattable interpolation de Lagrange, qui avec un nombre suffisant de termes donne une loi exacte, pour toutes les planètes connues (mais pour les planétoïdes, c'est une autre histoire)
Bon, si après ça vous vous intéressez toujours à la loi de Bode, sachez que dès 1918, on admettait définitivement avec Max Wolf, qu'il existait bien deux populations de planètes dans le système solaire, les telluriques et les joviennes, qu'elles avaient des caractéristiques très différentes, et qu'il était dès lors vain de vouloir les rattacher à une loi unique
En tenant compte de ces deux populations, de la masse des planètes, de leurs vitesses et de leurs moments cinétiques, on a pu comme Evry Shatzman, trouver enfin des relations correctes dans la répartition des planètes.
En conséquence, avant de publier votre géniale loi, qui explique tout d'une seule formule, réservez lui sa place au cimetière... 
 |
 |
 |
 |
 |
|