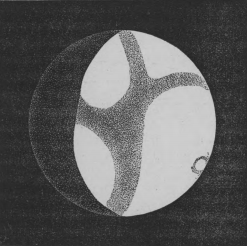
1884. Jean-Charles Houzeau baptise le satellite de Vénus.
 Jean-Charles Houzeau |
En 1857, il part pour La Nouvelle-Orléans, où il fait simultanément de l'astronomie, de la météorologie, de la zoologie, et du journalisme. Dès 1861, il défend la cause des Noirs. Directeur du premier journal quotidien publié pour les noirs, il écrit des articles en faveur de l’abolition de l’esclavage. En 1868, il gagne la Jamaïque où pendant 7 ans il ne va plus guère s'occuper que d’astronomie.
En 1876, Léopold II lui offre le poste de directeur de l’Observatoire royal de Belgique, il rentre au pays et s’attèle à la modernisation de l'observatoire qu'il dirige jusqu'en 1883.
Jean-Charles Houzeau a publié en 1880 un Traité élémentaire de météorologie, mais les astronomes se souviennent surtout de sa bibliographie générale de l'astronomie compilée avec Albert Lancaster en 1887.
Nous allons voir ici la théorie originale (mais fausse) qu'il avait imaginé pour expliquer les apparitions épisodiques du satellite de Vénus. Il lui avait même trouvé un nom: Neith. Mais cette appellation n'a pas duré longtemps: 3 ans plus tard, Neith était renvoyée aux oubliettes par Stroobant.
|
Le satellite problématique de Vénus. Sept fois, depuis l'invention du télescope, on a aperçu à côté de Vénus un petit corps, qui présentait la même phase que la planète, et que l'on avait désigné comme son satellite, Mais ces observations étaient passagéres ; souvent dès le lendemain la petite étoile avait déjà disparu. C’étaient des apparitions à de longs intervalles ; il y a maintenant 120 ans que la dernière a été notée. Etait-on en présence d'illusions? Il n'est guère permis de le croire, car toutes ces observations ont été faites ou par des astronomes célèbres, tels que Dominique Cassini, ou du moins par des astronomes exercés.Note: Nul n'est infaillible, Fontana n'était qu'un hableur, et le satellite de Vénus disparut avec le progrès des instruments comme l'avait fait remarquer Proctor. S'agissait-il d'un satellite, qui n'aurait brillé que dans des circonstances accidentelles ? On peut encore répondre par la négative, d’abord à cause de l'impossibilité de représenter convenablement les positions observées par une orbite décrite autour de Vénus, et ensuite parce que la masse de cette planète, déduite des essais les moins défectueux, serait sept fois ce qu'elle est en réalité. Mais si ce prétendu satellite n’en était pas un, que faut-il penser de ces apparitions fugitives ? Il y a quatre ans, dans une lecture faite à l’une des séances publiques de l'Académie de Belgique, j'ai exprimé le doute que le satellite problématique de Vénus fût une planéte intra-mercurielle, Qu'une petite planète, circulant en dedans de l'orbite de Mercure, se trouve un jour dans un assez grand rapprochement apparent de Vénus pour paraître dans le champ de ja lunette avec elle, et l'on verra à côté du disque considérable de Vénus un corps de dimensions moindres, présentant une phase peu différente de celle de la grande planète, C’est précisément ce qu’on avait observé. Il y avait un moyen de décider si cette explication était admissible. Une planète intra-mercurielle ne peut pas s’écarter du Soleil autant que le fait Vénus ni même Mercure. Elle ne pouvait donc être vue près de la première de ces planètes qu'aux époques où celle-ci, dans son mouvement apparent, n'est pas encore fort éloignée du Soleil. Si l'observation avait parfois été faite à des distances du Soleil égales ou supérieures aux plus grandes digressions de Mercure, il faudrait chercher une autre hypothèse. Eh hien, l'examen des données montre précisément que, dans toutes les circonstances où l'on a cru voir près de Vénus une petite étoile accompagnatrice, ayant une phase comme la grande, ces astres étaient éloignés du Soleil à une distance qu'un corps contenu dans l'orbite de Mercure ne peut pas atteindre. L'explication à laquelle j’avais cru un moment qu'il serait possible de recourir est donc absolument inadmissible. Il faut renoncer à cette idée, et je tiens d'autant plus à le dire que je l'avais moi-même proposée. Le tableau ci-dessous présente les dates auxquelles on a cru voir le satellite problématique de Vénus, avec les élongations correspondantes de la planète, et ses distances à la Terre :. TABLEAU I
Note: Ce tableau montre effectivement des élongations trop fortes pour une planète intramercurielle, mais il montre aussi que Houzeau a sélectionné les observations qui l'arrangeaient, même si elle ne prétendaient pas être celle d'un satellite, comme celle de Fontana, et négligé d'autres observations comme celle d'Andreas Mayer, du père Lagrange ou de Horrebow. Mais en la soumettant à la critique, l'examen des observations a indiqué, au lieu de la confirmation que j'y cherchais, une très-curieuse coïncidence, d'un ordre tout différent, dont je vais essayer de montrer d'un côté la vraisemblance, et de l'autre, je me hâte de le dire, les difficultés. Formons le tableau des dates, n'en prenant qu'une pour 1764, où les deux observations appartiennent à une seule approche mutuelle des deux corps Ces dates se voient ci-dessous, en années et partie d'années. La troisième colonne présente les intervalles qui les séparent. Le moindre est le dernier. 2ans,90. Supposant que cette durée marque une période qui ramène le rapprochement des deux corps, nous devrons retrouver, dans les autres intervalles, des multiples de cette quantité. Chaque intervalle en particulier donnera même une valeur de la période, parce que nous connaîtrons le nombre des retours. Toutes les valeurs ainsi obtenues figurent dans la dernière colonne du tableau ci-joint. La ligne finale présente le résultat déduit de l'intervalle total. TABLEAU II
Note: Cette concordance est surtout l'effet de la sélection des données. Voilà deux corps, l’un relativement grand, l'autre qu'on décrit comme présentant des dimensions beaucoup moindres, qui, à des intervalles à peu près fixes, se retrouvent côte à côte. Mais puisque dans les intervalles ils sont séparés, il ne s'agit pas d'un véritable satellite. Ce qui ressort des faits, c'est que les routes qu'ils suivent les ramènent ensemble à des intervalles déterminés. Ces routes sont voisines l'une de l'autre dans toute leur étendue, car des conjonctions ont été observées dans différentes parties de l'orbite de Vénus, en deça et au delà du Soleil, à l’orient et à l'occident de cet astre. On ne satisfait à ces conditions qu'en imaginant deux orbites sensiblement concentriques, et d’un rayon fort peu différent. Note: Pas besoin d'être astronome, même amateur pour réfuter cette hypothèse. Un simple curieux du ciel, avec un bon manuel d'astronomie comprendrait que cette planète, d'une taille intermédiaire entre la Lune et Mercure, serait visible à l'oeil nu comme une étoile de première magnitude. Elle serait donc connue depuis l'antiquité. Pour abréger, je me permettrai de désigner par un nom l’astre problématique dont je vais avoir tant de fois à parler. Toute appellation remplirait le but : je choisis Neith, nom de la déesse mystérieuse de Saïs, dont aucun mortel n'avait soulevé le voile. Je dirai donc : Vénus et Neith reviennent en conjonction apparente tous les 2ans,96, c'est-à-dire au bout de 1080 jours environ, dans leurs orbites concentriques très-voisines. C'est évidemment que Neith va plus vite ou moins vite que Vénus, et qu'après avoir gagné ou perdu une révolution, el'e se retrouve finalement à la même longitude avec cette dernière. En 1080 jours Vénus décrit autour du Soleil 4 circonférences entières + 290°. Examinons quelles seraient les conséquences si Neïth décrivait, dans le même intervalle, soit 5 circonférences + 290°, soit 3 circonférences + 290°. Désignons ces hypothèses par les lettres À et B. TABLEAU III
Note: Et nous pouvons rejeter la seconde pour la raison de visibilité à l'oeil nu vu plus haut. La 2e et la 4e observation ont été faites dans des positions presque identiques de la Terre par rapport au Soleil et à Vénus : les élongations et les angles à Vénus étaient à bien peu près les mêmes. Si nous comparons entre elles ces deux dates, nous trouvons un intervalle de 68ans,74 pour 23 périodes, d'où chaque période serait de 2ans,99 ou de 1092 jours. Il ne paraît pas que ce chiffre doive être subdivisé, et soit multiple de la période véritable, car cette circonstance exigerait d'éloigner davantage l'orbite de Neith de celle de Vénus, soit en dedans soit en dehors, et conduirait à des difficultés insurmontables. En eflet, en dedans de l'orbite de Vénus, les digressions manqueraient de plus en plus à satisfaire aux observations nos2 et 4; et en dehors de cette orbite, les conjonctions géocentriques s'écarteraient de plus en plus des conjonctions héliocentriques, et fausseraient la régularité apparente de la période. Au contraire, tant que les deux orbites sensiblement concentriques restent fort voisines, les instants des conjonctions géocentriques ne différent pas beaucoup de ceux des conjonctions héliocentriques, et la période apparente, celle que nous constatons, demeure sensiblement uniforme, ainsi que le donnent les observations. Mais voici une circonstance curieuse et qui offre un rapprochement d'une autre espèce et complétement inattendu. Dans la supposition qu'une planète circule autour du Soleil, un peu en dehors de l'orbite de Vénus, elle doit être soumise à des perturbations considérables de la part de ce dernier astre. Afin de nous former une première idée de l'importance qu'elles peuvent acquérir, cherchons, comme on le fait en pareille circonstance, s’il existe un rapport, au moins très-approché, entre deux multiples des durées des révolutions. Voici les premières lignes du tableau dressé dans ce but : TABLEAU IV
Note: Et voila comment on retombe sur ses pattes: au lieu de réfuter la théorie, les anomalies la confortent. Mais si on suppose l'égalité exacte, il y a lieu d'en examiner les conséquences en les comparant aux observations. Le fait que des perturbations analogues n'ont pas été reconnues dans la marche de Vénus, et sont par conséquent fort peu sensibles pour cette planète, indique seulement l'exiguité de la masse de Neith, et n’a rien qui soit inadmissible. La presque égalité des nombres cités est au contraire fort remarquable, en ce qu'elle atteste un rapport qui a fini peut-être par s'établir exactement. Note: Si la masse de la planète est négligeable, sa taille est alors trop petite pour expliquer que les observateurs ont tous décrit une taille similaire à celle de la lune. Sans accorder plus d'importance qu'elles n'en méritent à ces réflexions encore conjecturales, n'y a-t-il pas, dans ce qui précède, de singulières coïncidences, qui paraissent, surtout lorsqu'on les prend dans leur ensemble, dépasser les effets ordinaires du hasard ? Une planète de petite dimension, une sorte de satellite échappé, marcherait pour ainsi dire sur les pas de Vénus, mais en perdant sans cesse sur elle, pour revenir en conjonction tous les 3 ans environ. Note: Dans un livre de Jules Verne, cela passerait parfaitement. Si nous ajoutons à la dernière date de 1764 soit 40 soit 41 périodes, nous arrivons à peu près à l'époque actuelle ; mais l'intervalle étant de plus d'un siècle, il est impossible de préciser le moment de la conjonction.
Note: Cette apparition d'une petite tache sur le disque de Vénus fait tellement penser aux observations de Fontana qu'elle incite la méfiance. Selon Stroobant, il est prouvé que ce n'était effectivement qu'une tache sur Vénus. Après avoir indiqué des rapprochements qui sont au moins singuliers, il me reste à mentionner une difficulté qu'offre notre hypothèse, L'inclinaison de l'orbite de Vénus, sans être bien grande, est pourtant sensible. Les observations de l'astre problématique ont été faites à des distances diverses du nœud de Vénus, et par conséquent dans des points où les orbites auraient dû se séparer en latitude. Cependant, pour avoir les deux corps en même temps dans le champ d'une lunette, il ne pouvait pas exister entre eux d'écart supérieur à ½° environ. Si, dans le tableau I, on jette les yeux sur les latitudes géocentriques de Vénus, lors des diverses observations, on voit qu'elles affectaient des valeurs très-irrégulières. Pour conserver la proximité apparente, il faut admettre, ce qui serait extrêmement improbable s'il s'agissait de planètes prises au hasard, que les deux lignes des nœuds ainsi que les deux inclinaisons sont très-voisines, en d'autres termes que les plans des deux orbites sont à peu près confondus. Cette circonstance n'est pas toutefois aussi extraordinaire qu'elle paraît d'abord, si l'on réfléchit que l'orbite de Neith est sous l'influence directe de celle de Vénus, qui en est notablement rapprochée. Considérant l'orbite de Vénus comme la démarcation de l'équateur d’un corps central, dont le ménisque serait réparti sur cette orbite, Neith représenterait un satellite, circulant à faible distance, et l'attraction du ménisque maintiendrait le corps dans le plan susdit. L'objection n'a donc pas autant-de valeur qu’on l'aurait pensé au premier abord, et il n'ÿ aurait ici rien d’étrange à voir les plans des deux orbites sensiblement communs. Si l'on pouvait éloigner un peu la Lune de la Terre, et la placer à un moment donné en opposition, elle cesserait de circuler autour de notre globe, et ferait sa révolution comme nous autour du Soleil. Qui peut affirmer qu'un cas de ce genre ne s’est pas présenté pour Vénus,et que Neith n'est pas comparable à ce que je nommerai un pseudo-satellite, placé au-delà de la sphère d'attraction de Vénus? Note: Cette hypothèse du pseudo satellite est, en soi, intéressante, et complète l'idée qu'avait déjà eu Short, que le supposé satellite était en fait une planète. Malheureusement, elle s'effondre à l'examen. J. C. HOUZEAU.
(1) M. Houzeau n’avait pas connaissance de ces observations lorsqu'il a rédigé sou article. Le paragraphe qui les mentionne a été intercalé après coup.Note de la Rédaction. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ( J. C. HOUZEAU, Le satellite problématique de Vénus, Ciel et Terre, 1884, p. 121-129 ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Jean-Charles Houzeau n'était plus directeur de l'observatoire royal de Belgique, quand il a publié cette théorie, mais il était membre du comité de rédaction de la revue Ciel et Terre, et son aura d'ex-directeur a permis que ce texte soit publié dans d'autres revues comme Cosmos, ou l'Astronomie, et critiquée dans The Observatory.
Il n'empêche que ce texte est un bel exemple de pseudoscience: Houzeau a sélectionné les données qui l'arrangeaient, valorisé les arguments qui le confortaient, déprecié ou ignoré les arguments qui le réfutaient, bref il s'est conduit comme un astrologue. Hé oui!
Devons nous lui mettre un bonnet d'âne  ou un chapeau d'astrologue
ou un chapeau d'astrologue  ?
?
| Accueil | Sciences | Astronomie | Erreurs | satellite de venus | le retour |