Un demi siècle pour découvrir l'anneau de Saturne (les aspects télescopiques sont représentés pour un écran 17" en 800x600) (les dessins de Saturne ont été reproduits horizontalement, à la même échelle) 1610, (date exacte incertaine) dessin de Galilée A Padoue, Galilée découvre que Saturne est flanqué de deux appendices, qui ne se comportent pas comme des satellites. Il en parle pour la première fois dans une lettre datée de Juillet Tous les manuels d'astronomie montre le dessin de gauche, mais il faut se rappeler que la lunette de Galilée ne grossissait que 20 fois. En remettant l'image à l'échelle, Galilée a du observer quelque chose comme l'image de droite Il ne pouvait donc pas comprendre qu'il s'agissait d'un anneau ce que voyait Galilée 1612 Les appendices disparaissent pour Galilée (l'anneau est vu par la tranche). Galilée, qui ignore que la disparition n'est que temporaire, cesse de surveiller Saturne pendant quelque temps 1614 dessin de Scheiner Le père jésuite Christoph Scheiner, qui découvrit les taches solaires en même temps que Galilée, observe lui aussi Saturne et le dessine. On peut supposer que la lunette qu'il utilisait à cette époque était de puissance comparable à celle de Galilée. Il fut cependant le premier à utiliser dès 1615, une lunette à oculaire convergent selon le principe énoncé par Képler en 1611 le père Scheiner 1616 dessin de Galilée A gauche, nouveau dessin de Saturne par Galilée. Il en publiera une gravure en 1623 dans il saggiatore (l'essayeur) Si Galilée utilisait alors la plus puissante lunette qu'il eut, qui grossissait 30 fois, voici à droite ce qu'il pouvait voir On note ses qualités d'observateur, capable d'interpréter correctement une image aussi petite ce que voyait Galilée avant 1620 dessin de Biancani Le père jésuite Giuseppe Biancani, qui publiera en 1620 Sphaera mundi, seu Cosmographia demonstrativa..., dessine Saturne avec deux satellites reliées par des anses. livre de Biancani 1633 dessin de Gassendi Gassendi et Saturne ↑ lire le dossier ↑ Pierre Gassendi, plus connu comme philosophe et disciple d'Epicure que comme astronome, entreprend d'observer Saturne. Ses observations vont s'échelonner de 1633 à 1655, l'année de sa mort. Pendant cette période il verra Saturne sous les aspects les plus divers et en fera pas moins de 23 dessins. Il semble d'ailleurs ètre le premier à avoir dessiné Saturne sans anses, en 1642. Il mourra quelques mois avant que Saturne ne retrouve cette apparence, sans en avoir compris le mystère, et au moment même ou Christian Huygens en découvre la solution. Son problème fut de n'avoir pu, comme Huygens, fabriquer ses objectifs de lunette lui même, et d'avoir du observer toute sa vie avec des instruments trop faibles. De même ses nombreuses mesures de position ne furent jamais utilisées, car bientôt, la précision des mesures décupla, rendant les siennes obsolètes 1640 dessin de Riccioli Le père jésuite (hé oui, ils étaient partout) Giovanni Battista Riccioli, qui s'illustrera plus tard en publiant l'Almagestum novum, contenant une carte de la lune, dessine Saturne avec deux appendices séparés livre de Riccioli 1645 Le capucin tchèque Anton Maria Schyrleus, dit père de Rheita, publie Oculus Enoch et Eliae, siue, Radius sidereomysticus. De Rheita est l'inventeur du "redresseur", une lentille intermédiaire qui permet de voir l'image à l'endroit dans une lunette. Dans son ouvrage il admet que Saturne a bien deux compagnons, et qu'alors ils devraient ètre périodiquement éclipsés par la planète, ce qu'on n'aurait jamais observé. Il en déduit, soit qu'ils effectuent leur révolution indépendamment de Saturne, soit qu'ils brillent d'une lumière propre et éclairent Saturne, qui en a bien besoin car elle est cent fois moins éclairée par le soleil que la Terre. Cette hypothèse est pour lui quasi-certaine Bien sûr, son idée ne tient pas debout puisque les "compagnons" disparaissent bien tous les quinze ans, et ne sont pas plus lumineux que Saturne. De plus leur luminosité propre ne mes empécheraient pas de tourner autour de Saturne et d'ètre éclipsés livre de de Rheita 1646 dessin de l'ouvrage dessin du 3/12/1645 Francesco Fontana, premier italien à utiliser des oculaires convexes, publie Novae coelestium terrestriumque rerum observationes., où il présente ses observations faites "specillis a se inventis" (avec des verres inventés par lui). Hélas, n'est pas Galilée qui veut. Son dessin de Mars est un cas d'école pour s'initier aux aberrations des instruments, et les anses de Saturne qu'il dessine sont assez fantaisistes. Du moins, il les dessine livre de Fontana 1647 dessin d'Eustachio Divini Eustachio Divini dessine un anneau tangent à la planète Là aussi, il faut tenir compte du grossissement des instruments de l'époque. Celui d'Eustachio Divini grossissait à peine 60 fois Cependant il prétendra plus tard que la lunette, plus puissante, de Huygens donnait une image fausse, puisqu'elle montrait ce qu'il ne voyait pas (objection qu'on avait faite à Galilée, dont la lunette montrait des étoiles invisibles à l'oeil nu) ce qu'il voyait 1647 René Descartes René Descartes, après avoir inventé son système très personnel des tourbillons, où la terre était immobile dans un tourbillon mobile, veut que son système ait réponse à tout. Aussi prétend il vouloir expliquer l'immobilité des pseudo-satellites observés par Galilée. Dans la troisième Partie de la seconde édition de ses Principes de la Philosophie, il attribue, l'état stationnaire de ces prétendus satellites à ce que Saturne présente toujours la même face au centre de son tourbillon. Malheureusement,entretemps, les compagnons de Saturne s'étaient mués en anses qui avaient déja eu le temps de disparaitre trois fois tourbillons de Descartes 1650 dessin de Riccioli le père Giovanni Battista Riccioli, dessine lui aussi un anneau tangent La comparaison avec les autres dessins laisse supposer qu'il utilisait une lunette plus puissante qu'en 1640 1655, 25 mars dessin de Huygens Le 25 mars, vers 8 heures du soir, Christian Huygens pointe sa lunette de 12 pieds vers Saturne. Il observe Saturne avec deux "bras" (brachii). A droite, ce qu'il pouvait voir avec le grossissement de 50 de sa lunette ce que voyait Huygens 1655 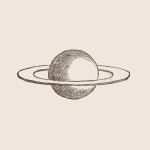schéma de Huygens Christian Huygens découvre la vraie géométrie de l'anneau. Constatant la révolution de son satellite en 16 jours, il en déduit que Saturne doit aussi tourner sur son axe. Argument: toutes les planètes doivent tourner sur elles même afin que toute leur surface jouisse de la lumière du soleil. ( atque ita tota eorum superficies lumine solis per vices gaudeat ) C'est l'argument boiteux des "causes finales", mais la conclusion est tout de même exacte. Il en déduit que puisqu'il observe la même apparence de "bras" malgré la rotation, c'est que ces bras forment en réalité un disque plat vu par la tranche. Et comme les anciennes observations montrent un espace entre les anses et le globe de la planète, c'est que ce disque n'est pas tangent à la planète mais forme un anneau 1655 Hodierna Giovanni Battista Hodierna dit avoir vu Saturne, avec deux petites boules, la plus à l'est étant plus petite, alors que Huygens, à la même époque, observait Saturne, avec deux "bras" égaux. Auteur de De systemate orbis cometici; deque admirandis coeli characteribus, contenant une liste de 40 objets célestes, Hodierna pensait que Saturne était en forme de ballon de Rugby, avec des taches noires. Sa lunette grossissait 20 fois. Connaissant l'ouverture des anneaux à cette époque, nous pouvons reconstituer ce qu'il voyait: quasiment rien du tout ce que voyait Hodierna 1656 dessin de Huygens De janvier à octobre, les "bras" ne sont plus visibles pour Christian Huygens. Saturne lui apparait "ronde". Sa lunette d'alors est nettement meilleure que celle de Galilée: 7 mètres de long avec un objectif diaphragmé à 60 mm et un grossissement de 90 ce que voyait Huygens Quatre théories en trois ans 1656, 25 mars Pour prendre date, Huygens publie sa découverte sous forme d'un anagramme: aaaaaaacccccdeeeeeghiiiiiiillllmmnnnnnnnnnooooppqrrstttttuuuuu qui cache la phrase suivante: Annulo cingitur, tenui, plano, nusquam cohaerente, ad eclipticam inclinato (Elle est entourée par un anneau, mince, plat, nulle part attaché, incliné sur l'écliptique) 1656, août hypothèse de Roberval Gilles Personne de Roberval, professeur au collège royal (et inventeur de la fameuse balance) imagine que les appendices sont des nébulosités s'élevant très haut depuis les régions équatoriales de Saturne. Cette hypothèse, qui rappelle un peu l'explication des comètes par Aristote, explique à la rigueur les variations d'apparences selon l'inclinaison, mais pas les lacunes à l'intérieur des anses Roberval 1656 Johannes Hevelius Johan Hewelcke, en latin Johannes Hevelius, publie à Dantzig, "de nativa Saturni facie" (de l'apparence réelle de Saturne). Il suppose que les "anses" sont en fait deux croissants attachés à un corps central ellipsoïdal, dont la rotation suivant le petit axe explique les variations d'apparence de Saturne, des anses aux deux petits disques Ce système n'explique pourtant pas les apparences de "bras"  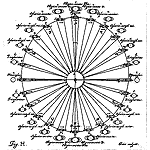 ↑ cliquez pour agrandir ↑ 1658 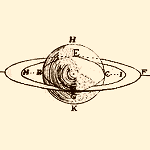système de Wren Christopher Wren, l'architecte de la cathédrale St Paul de Londres, suppose un anneau elliptique tangent très mince expliquant les disparitions périodiques Cette fois, les apparences de "bras" sont expliquées par l'aplatissement apparent du à la perspective Mais Wren, l'architecte, a visiblement du mal à concevoir un anneau qui tienne tout seul sans point d'attache Christopher Wren 1659, 12 février dessin de Huygens Le 12 février, vers 6 heures du matin, Huygens observe et dessine Saturne avec les anses nettement ouvertes. A droite, ce qu'il pouvait pouvait voir avec le grossissement de 90 de sa lunette de 7 mètres Cette observation, dernière qu'il mentionnera dans son livre, confirme clairement son interprétation ce que voyait Huygens 1659, 28 juillet Christian Huygens Christian Huygens publie "systema saturnium" où il présente ses observations de Saturne et de son satellite (Titan), et explique correctement la disparition périodique des anneaux. 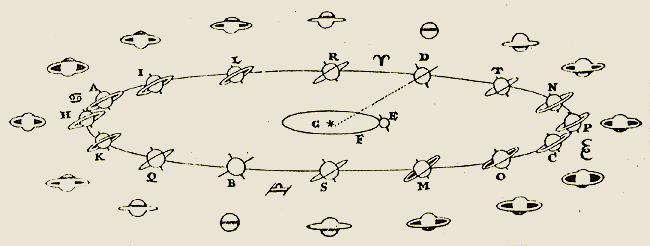Il présente aussi les observations de ses prédécesseurs, et c'est de son livre que viennent la plupart des dessins publiés Le livre de Huygens Position de Saturne dans l'espace, et aspect correspondant vu de la Terre, d'après Huygens Ainsi, la géométrie de ce qui avait été découvert en 1610, n'est clairement expliqué qu'en 1659. La première tentative (géniale) pour expliquer ce mystérieux anneau apparaitra l'année suivante