Histoire de la mesure de la vitesse de la lumière Le temps des spéculations On sait depuis la plus haute antiquité que l'éclair est perçu avant le grondement du tonnerre, mais on l'interprétait souvent en disant que "la vue est plus prompte que l'ouïe". Car dans l'antiquité on avait une notion très subjective de la vision. La notion moderne des images n'est apparue qu'avec l'étude de la perspective, corroborée par la découverte de la chambre noire. Dans l'antiquité, donc, on n'imaginait pas la lumière se projetant pour former des images, mais la vision émanant de l'oeil pour capturer des images inhérentes à l'objet. Il y a plus de 25 siècles, les philosophes présocratiques malgré leurs intuitions géniales, n'avaient qu'une notion très flou du phénomène de la vision, qu'ils essayaient de rapporter aux quatre éléments. Ainsi Démocrite d'Abdère pensait que l'oeil est fait d'eau, à cause de sa réflexion vitreuse, mais Empédocle d'Agrigente, le pensait de feu, à cause des phosphènes. On était donc loin d'imaginer que les images ne se forment que par projection sur notre rétine. Le seul qui ait fait un premier pas sur la bonne voie, est précisément Empédocle, qui, selon Aristote, pensait tantôt que la vision émane de l'oeil, et tantôt qu'elle émane des objets visibles, en laissant entendre que la transmission des objets à l'oeil n'était pas instantané, mais progressive. En langage moderne, nous dirions que cela impliquait que la lumière avait une certaine vitesse. Après les présocratiques, viennent immanquablement Platon et Aristote. Platon Aristote Platon explique la vision par le feu, le plus subtil des éléments. Mais plutôt qu'imaginer que la lumière est faite d'un feu qui atteint notre oeil, il invoque l'intéraction d'un feu extérieur, émis par les objets lumineux, avec un feu intérieur émis par l'oeil de l'observateur, et qui ainsi provoque la vision. Aristote, lui, juge absurde l'idée d'une vision issue de l'oeil qui irait jusqu'aux étoiles. Si la vision émane de l'oeil, pourquoi l'oeil ne peut il voir dans le noir? Pour Aristote la vision découle de la propriété qu'on les objets visibles de transmettre leur lumière à l'oeil par l'intermédiaire d'un milieu qu'il appelle "diaphane". Et cette transmission est instantanée car la lumière n'est pas un mouvement. Il n'est donc pas question d'imaginer une vitesse de la lumière. Au siècle suivant Euclide n'est pas loin de découvrir le sténopé et la projection des images. Mais il s'arrète à la propagation des rayons de lumière en ligne droite, fait démontré par les ombres, et ne se préoccupe ni de la nature, ni de la vitesse de la lumière. Ce sera tout de même le fondement de l'optique géométrique. Encore deux siècles et Lucrèce nous explique le point de vue des atomistes. La vision est provoquée par la perception de "simulacres", sortes de membranes impalpables entourant les objets, donc de leur formes exactes, et émises en permanence. Leur vitesse est très grande car un miroir nous montre instantanément la lumière des étoiles. Lucrèce n'imagine donc pas que les images se forment à la récéption de la lumière, mais au contraire à son émission. Sa théorie parait en retard sur Euclide. Finalement, l'intuition d'Empédocle fut réduite au silence par l'autorité d'Aristote, dont l'interprétation fit autorité dans le monde Chrétien jusqu'au XVIème siècle grâce aux commentaires de St Thomas d'Aquin C'est donc dans le monde musulman que réapparait, au XIème siècle, l'idée d'Empédocle avec Ibn Sînâ, dit Avicenne, l'astronome persan Al Biruni, et surtout Ibn al Haytham, dit Alhazen, qui dans ses différents traités d'optique, pose le problème sous sa forme moderne, en séparant nettement la propagation de la lumière et la vision des objets. Dans ce cadre on peut se poser la question de la vitesse de la lumière. Le problème réapparaît dans le monde chrétien au XIIIème siècle, avec Robert Grosseteste, Roger Bacon, et John Pecham: Le premier pense toujours que la lumière est émise par l'oeil, le second qu'elle est à la fois émise et reçue, et le troisième qu'elle est seulement reçue. Dans le cadre de la réception, Bacon et Pecham supposent une propagation à vitesse finie. Bacon, qui semble reprendre les idées d'Empédocle, écrit au chapitre Perspectiva: Si ergo lucis multiplicatio est in instanti et non in tempore erit instans sine tempore quia tempus non est sine motu. Sed impossibile est instans esse sine tempore sicut nec punctum sine linea Si donc la propagation de la lumière se faisait instantanément et non temporellement, il y aurait instant sans temps, parce que le temps n'existe pas sans mouvement. Mais l'instant sans le temps est aussi impossible que le point sans la ligne Cependant, au XVIIème siècle encore, quelques savants, et non des moindres, croyaient encore la propagation instantanée Ainsi, Képler admet bien le caractère géométrique de la propagation de la lumière, avec comme conséquence une diminution d'intensité selon l'inverse du carré de la distance, mais croit cette propagation instantanée, et Descartes, qui pourtant, a découvert les lois de la réfraction, est du même avis Les premières tentatives de mesure A la fin du moyen age, plusieurs opticiens pensaient que la lumière avait une vitesse, mais personne n'avait tenté de le vérifier. Il fallut attendre l'avènement de la science expérimentale. l'expérience des lanternes le texte des discours ↑ lire le dossier ↑ C'est donc Galilée qui, le premier, chercha à mesurer cette vitesse. Il imagina une expérience, qu'il décrit dans Discours Et Demonstrations Mathematiques Concernant Deux Sciences Nouvelles. Deux personnes postées à bonne distance l'une de l'autre se font des signaux lumineux, en masquant et démasquant des lanternes, l'un démasquant sa lanterne aussitôt qu'il aperçoit le signal de l'autre lanterne. Il imagina même, si besoin était, d'opérer à grande distance, en utilisant des lunettes installées avec les lanternes dans de petits observatoires Il semble que Galilée ait bien réalisé cette expérience, en plaçant des aides à quelques centaines de m l'un de l'autre, puis en augmentant la distance, sans dépasser un mille. Mais les durées mesurées étaient indépendantes de la distance, et ne correspondaient qu'au temps de réaction des faiseurs de signaux. Nous savons aujourd'hui que, même avec deux observateurs munis de lunettes (astronomiques, bien sûr), le résultat eut été équivalent Plus tard les membres de l'académie "del cimento" de Florence, opérant sur une distance plus grande, n'eurent pas plus de succès. De telles expériences paraissent aujourd'hui bien naïves, mais à l'époque, on n'avait pas la moindre idée de l'ordre de grandeur de ce qu'on cherchait à mesurer. Pourtant, on aurait pu comprendre l'inutilité d'expériences faites à notre échelle, en réfléchissant à ce que, si la vitesse de la lumière avait été perceptible à cette échelle, alors elle eut été une vitesse de tortue à l'échelle du système planétaire, ou les distances sont jusqu'à un milliard de fois celle sur laquelle expérimentait Galilée, avec pour conséquence que les variations de distance, ne serait ce qu'à cause du mouvement de la Terre, aurait produit des écarts de plusieurs années dans l'observation des phénomènes, les rendant incompréhensibles et imprédictibles. Notons que la vitesse de la lumière est nécessairement supérieure à celle de la Terre sur son orbite, sans quoi la nuit, toute une partie du ciel, celle qui est à l'opposé du mouvement de la Terre, paraitrait obscure, puisque la lumière issue des étoiles ne parviendrait pas à rattraper la Terre. A l'époque de Galilée, on pensait que le Soleil était (en unités de l'époque) à environ 7.5 millions de km de la Terre. On pouvait en déduire une vitesse de la Terre sur son orbite d'environ 1500 m/s. Ceci était encore mesurable par la méthode de Galilée, mais il n'aurait probablement pas tenté son expérience s'il avait su que la vitesse réelle de la Terre est 20 fois supérieure. Galilée ne mesura donc rien du tout. Il n'en déduisit pas pour autant que la propagation était instantanée, il en déduisit que si la vitesse de la lumière avait une valeur finie, cette valeur était très grande, et la propagation quasi instantanée à notre échelle René Descartes Pierre de Fermat Pierre de Fermat (l'auteur du théorème) et René Descartes en discutèrent. Fermat fit remarquer que Galilée eut été mieux inspiré d'utiliser un miroir plutôt qu'un aide, supprimant ainsi le retard dû à son temps de réaction. Aujourd'hui, cette idée paraît évidente, mais il faut se rappeler qu'à l'époque, la qualité des miroirs n'aurait probablement pas permis l'expérience. Et d'ailleurs, Galilée n'aurait probablement pas réussi à l'aligner correctement. Mais cette idée d'un aller et retour après réflexion fut utilisé par Mersenne pour mesurer la vitesse du son, à l'aide de son écho Quant à l'idée du miroir, elle fut reprise deux siècles plus tard (avec celle de la lunette), dans la méthode de la roue dentée. Descartes, qui, dans le cadre de sa théorie d'un éther mécanique, croyait à la propagation instantanée, objecta que si la vitsse de la lumière était finie, comme Galilée avait tenté de le démontrer, alors les éclipses de lune se produiraient avec avance ou retard, car la distance de la lune n'est pas constante. Or les éclipses se produisaient au moment prévu, donc la propagation était instantanée Mais Fermat expliquait la réfraction de la lumière par un principe de moindre temps de parcours. Et donc, le temps de propagation ne pouvait être nul Et comme le remarqua Huygens, l'objection de Descartes, ne prouvait nullement l'infinitude de la vitesse de la lumière, et ne définissait en fait qu'une limite inférieure, tout comme l'expérience de Galilée. En 1677, Huygens put préciser que l'objection de Descartes imposait à la lumière une vitesse 100 000 fois supérieure à celle du son. Cependant, la remarque de Descartes allait être brillamment utilisée en sens inverse par Roemer. La première estimation Simon Marius Galilée Dès janvier 1610, Galilée et Simon Marius avaient découvert les quatre gros satellites de Jupiter. Ils semblent que chacun ait ignoré les observations de l'autre, mais c'est Galilée qui publia ses observations le premier. Pour mieux étudier le mouvement de ces satellites, Galilée avait même construit un ingénieux appareil: le "Jovilabe". Ces satellites montraient un ballet régulier, avec passages, éclipses, immersions fans l'ombre et émersions. Ces phénomènes paraissant bien prédictibles auraient du pouvoir servir à régler les horloges sur eux, et par là, de déterminer les longitudes. En effet il faut se rappeler que si les latitudes peuvent se calculer simplement en mesurant la hauteur des étoiles sur l'horizon, le calcul de la longitude nécessite d'observer l'heure à laquelle elle passe au méridien, dans la référence horaire du méridien d'origine (c'est à dire aujourd'hui, le Temps Universel). Galilée, Simon Marius et Hodierna s'attelèrent à la rédaction de tables, capables de prédire les configuration des satellites. Mais Hodierna utilisa trop peu d'observations, Simon Marius, échaudé d'avoir été devancé pour la découverte, publia trop vite, et Galilée, malgré la collaboration des savants hollandais, ne put achever ses travaux, car il devint aveugle. En 1668, Jean Dominique Cassini, qui observait alors en Italie, s'attaque au problème, et publie ses Ephemerides Bononienses mediceorum syderum, donnant les heures des phénomènes des satellites qui eussent pu servir à régler les horloges. les tables de Cassini pour 1676 En 1669, appelé en France par Colbert pour s'occuper de l'observatoire de Paris, que venait de fonder Louis XIV, il continua ses observations, et travailla à perfectionner ses tables, qui, pensait il, permettraient enfin de déterminer les longitudes de façon correcte, car selon lui, les prédictions faites sur les hypothèses de Galilée étaient très erronées, différant des heures réelles de "jours et heures" En 1676, Il publia ainsi dans Le Journal des sçavans une table des phénomènes de sortie du premier satellite de l'ombre d'août à décembre 1676. C'est sur la base des différences par rapport à cette table que la vitesse de la lumière a pu être mise en évidence. Roemer ou Cassini? Ole Roemer Jean Dominique Cassini On a longtemps, crédité l'astronome danois Ole Roemer de la découverte de la vitesse de la lumière. Aujourd'hui, la mode est d'en créditer Cassini. Mais la réalité est toute autre: c'est bien Roemer qui a fait la découverte effective, bien que ce soit Cassini qui l'ait mentionné le premier. Venu à Paris en 1672 avec l'abbé Picard, qui avait pu apprécier sa compétence lors de son voyage à Uraniborg, Roemer était partisan de la propagation successive de la lumière, et cherchait donc à la mettre en évidence. Il mit à profit son séjour à l'observatoire pour expérimenter l'idée de Descartes, et entreprit de la vérifier sur les satellites de Jupiter. Il trouva d'abord qu'au bout d'une révolution de Io, le premier satellite, on n'observait pas de retard sensible, bien que la distance de la Terre à Jupiter ait varié de plus de 210 diamètres terrestre. Mais pour une variation de distance nettement plus grande, il trouva que 40 révolutions observés lors d'une quadrature étaient plus courtes que 40 autres observées lors de la quadrature suivante. Il en déduisit que quand Jupiter est en conjonction, sa lumière doit, pour nous parvenir, mettre 22 minutes de plus pour parcourir une distance supplémentaire par rapport à l'opposition, égale au diamètre de l'orbite terrestre. La démonstration ↑ lire le dossier ↑ En Septembre 1676, il prédit ainsi pour une émersion de Io, un retard de 10 minutes par rapport à la prédiction de Cassini, retard qui fut effectivement observé le 9 Novembre. La démonstration de Roemer parut dans Le journal des sçavans du 9 décembre 1676 Ole Roemer prouva ainsi la "propagation successive" de la lumière, et Cassini admit que cela expliquait bien les inégalités dans le mouvement du satellite Io, mais il contesta la valeur du travail de Roemer, en objectant que cela n'était prouvé que pour le premier satellite de Jupiter (en fait il apparaît aussi sur les autres, mais moins visiblement car ils sont moins rapides). Cassini, lui, cherchait avant tout à améliorer sa méthode de détermination des longitudes par les éclipses des satellites, et pour cela à débarrasser ses tables des erreurs dues aux diverses "inégalités" qui apparaissaient dans le mouvement des satellites. Or à l'équateur, une erreur de 10 minutes de temps correspond à 150 milles marins. Une telle cause d'inégalités était donc impossible à ignorer Or, bien que les procès-verbaux des réunions de l'académie, de l'époque ne soient plus disponibles, Laurence Bobis et James Lequeux ont pu retrouver une copie, faite par Delisle avant 1738, d'une communication de Cassini, datée du 22 aout 1676. Cette communication est intitulée: Inégalités des satellites de Elle mentionne clairement que Cassini envisage la vitesse de la lumière comme explication d'une inégalité le passage clé de la lettre de Cassini, copiée par Delisle Alligata est haec irregularitas ad varietatem visibilis diametri jovis sive ad intervallum jovis a terra et videtur provenire ex eo quod lumen a satellitibus non perveniat ad nos nisi post motum ita ut impendat decem vel undecim minuta per spatium aequale semi diametro orbis annui Cette irrégularité est reliée à la variation du diamètre apparent de Jupiter, soit à la distance de Jupiter à la Terre et on voit qu'elle provient de ce que la lumière ne nous parvient d'un satellite qu'après le mouvement en sorte qu'elle demande 10 à 11 minutes pour l'espace égal au demi diamètre de l'orbite annuelle Mais il faut remarquer: - Qu'en aout 1676 , Roemer, qui était en France depuis 1672, et travaillait sur les données accumulées à l'observatoire depuis près de huit ans, avait eu le temps de parler de son travail. En particulier, découvrant les prédictions de Cassini, il est logique qu'il lui ai fait part de ses calculs, que Cassini ne pouvait pas ignorer puisqu'ils introduisaient une correction d'une dizaine de minutes dans ses tables. On comprend que Cassini se soit dépéché d'en faire part à l'académie, lui qui cherchait à présenter les tables les plus exactes possible, d'où sa communication faite 5 jours après la publication de ses tables. D'où l'antériorité de la communication de Cassini, sur la publication de Roemer - Que si Cassini fut un grand observateur (et un bon courtisan), il fut toute sa vie un infect théoricien: la Cassinoïde comparée à l'ellipse - en 1652, Cassini plaçait encore la Terre au centre du monde! 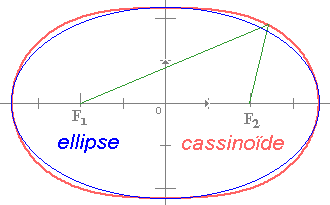- La même année 1652, il expliquait une comète par des émanations récentes provenant de la Terre et des autres planètes. - Il soutenait que Sirius était le centre des mouvements de la comète de 1664 - Il prétendait que les comètes étaient là pour donner aux hommes le goût de l’astronomie. - Vers 1680, Il prétendit remplacer les ellipses Képlériennes, qu'il n'admit jamais, par des Cassinoïdes, lieux dont le produit des distances (et non la somme) aux deux foyers est constant. Or, dans ses principia de 1687, Newton prouve que les ellipses de Képler s'accordent avec sa loi de gravitation en 1/r². La cassinoïde ne s'accorde donc pas avec la gravitation universelle, ressemble plus à une anse de panier qu'à une vraie ellipse, et ne donne des résultats acceptables que quand les foyers sont très rapprochés - en 1690, il abandonna la vitesse de la lumière qui ne suffisait pas à expliquer toutes les inégalités. Ceci implique qu'il ait pu croire qu'une seule cause les expliquait toute. En fait, si ses tables s'améliorent après 1693, ses calculs ne tiennent pas compte des perturbations de Saturne, ni de celles que les satellites exercent les uns sur les autres, et n'utilisent même pas les ellipses képlériennes - Que si Cassini avait effectivement découvert la vitesse de la lumière (qu'il ne cherchait pas), il en aurait revendiqué la paternité, car il ne se génait pas pour s'attribuer la paternité des travaux des autres, en particulier ceux de la mesure de la Terre par l'abbé Picard, qu'il prétendait avoir dirigé. Or, d'après ses publications successives: - en 1688, il défend sa méthode de calcul des longitudes contre Vossius, qui n'avait pas compris comment on pouvait utiliser les satellites de Jupiter pour calculer des longitudes terrestres, mais ne réclame rien pour la vitesse de la lumière - en 1693, dans un mémoire de l'académie des sciences, il explique: Monsieur Romer expliqua très ingénieusement une de ces inégalitez qu'il avoit observées pendant quelques années dans le premier satellite, par le mouvement successif de la lumière, qui demande plus de temps à venir de Jupiter à la Terre lorsqu'il en est plus éloigné, que quand il en est au plus près; mais il n'examina pas si cette hypothèse s'accomodoit aux autres Satellites qui demanderoient la même inégalité de temps ( Memoires de l'académie royale des sciences, tome VIII, page 317, Les hypothèses et les tables des satellites de Jupiter, réformées sur de nouvelles observations, la citation est page 391 ) Donc, c'est clair. Cassini n'a jamais prétendu avoir découvert la vitesse de la lumière, et ne s'y est intéressé que tant qu'il a cru pouvoir s'en servir pour améliorer ses tables. Ce n'est que d'un point de vue chronologique qu'il y a une antériorité de publication de Cassini sur Roemer. Or la communication de Cassini était manuscrite et immédiatement enregistrée, alors que celle de Roemer dut attendre sa publication dans Le journal des sçavans. On peut en conclure que dès qu'il a connu les résultats de Roemer, Cassini en a immédiatement tenu compte et fait une communication en conséquence Le népotisme contre Roemer Contre Roemer ↑ lire le dossier ↑ Ce n'est qu'en 1707, donc 31 ans après la découverte de Roemer, qui était rentré au Danemark depuis 26 ans, et 5 ans avant la mort de Cassini, qu'un article anonyme et tendancieux, de L'histoire de l'académie revendique pour Cassini la paternité de la découverte. Il se couvre de l'autorité de Maraldi, neveu de Cassini, auteur d'un article plus honnète paru dans les mémoires de l'académie. Mais il commet une erreur de date, qui place en 1674 la communication de Cassini, erreur qui est à l'origine de la légende. Or ceci est absurde, puisque Cassini n'aurait pas publié en 1676, des résultats qui ne tenaient pas compte d'une inégalité qu'il connaissait déjà en 1674. Le pire c'est que l'auteur anonyme est probablement Bernard Le Bovier de Fontenelle, secrétaire de l'académie des sciences à cette époque. Un Fontenelle qui, bien que connu pour sa longévité, n'avait que 19 ans à l'époque de la découverte, et ne devint secrétaire de l'académie des sciences que 16 ans après le départ de Roemer. Il faut reconnaitre que Fontenelle, plus connu pour ses magnifiques éloges des académiciens, fut bien mal inspiré. La première estimation numérique En dépit de la légende, Roemer ne put pas faire de vraie mesure, en effet l'ordre de grandeur du temps nécessaire pour parcourir le diamètre de l'orbite terrestre était connu, mais ce diamètre n'était lui même connu que par son ordre de grandeur. Les lois de Képler nous renseignant sur les dimensions relatives des orbites planétaires, mais pas sur leurs dimensions absolues. Roemer ne trouva donc que l'ordre de grandeur. (les valeurs qu'on cite aujourd'hui sont inventées, ou confondues avec celles de Huygens, elles même calculées a posteriori). l'abbé Picard Pourtant, un heureux enchainement de mesures aurait du permettre de connaître le diamètre de l'orbite terrestre. En 1670, remplaçant le comptage du nombre tours de roues d'un carrosse, par la méthode de triangulation qui venait de faire ses preuves en Hollande, l'abbé Picard mesura la longueur d'un arc de méridien entre Sourdon, près d'Amiens, et Malvoisine, au sud de Paris. Il trouva qu'un arc de 1° mesure 57 060 toises de Paris, d'où il put déduire la longueur du méridien complet, soit 9001.6 lieues, et enfin calculer la valeur du rayon terrestre: 1432.5 lieues, soit 6 372 km. Cette valeur était la première mesure sérieuse depuis celle d'Eratosthène, et sa précision était remarquable pour l'époque, puisque cela correspondait à un méridien de 40 001.7 km Puis en 1672, on réussit à mesurer la parallaxe de la planète Mars. Connaissant la valeur du rayon terrestre, ceci permettait d'en déduire la distance Terre-Mars, et de là, via les lois de Képler, la distance Terre-Soleil, et donc finalement la vitesse à laquelle la lumière traverse l'orbite terrestre. Malheureusement la petitesse de la parallaxe de Mars rendait les mesures difficiles, pour l'époque, et la réduction des observations fournit, pour la distance Terre-Soleil, des valeurs dispersées, qui, converties en km, étaient comprises entre 66 et 138 millions de km . C'est en 1690 qu'apparait la première estimation numérique sous la plume de Huygens. En reprenant le chiffre de 22 minutes, de Roemer, pour traverser l'orbite terrestre dont il estime le diamètre à 24 000 diamètres terrestre, il trouve, en simplifiant un peu, que la lumière parcourt 16 diamètres terrestres en une seconde, d'ou il déduit que la lumière se propage 600 000 fois plus vite que le son Il ne donne pas la vitesse, à proprement parler, mais mentionne que le diamètre terrestre est de 2865 lieues de 2282 toises, selon les mesures de l'abbé Picard. Ceci permet de trouver la valeur numérique: 45 840 lieues/s soit 204 000 km/s, avec le calcul simplifié, et 52 090 lieues/s, soit 230 000 km/s avec la mesure complète Accessoirement, nous en déduisons que Huygens estimait le rayon de l'orbite terrestre à 34.38 millions de lieues soit 153 millions de km, valeur nettement meilleure que celle de 1672 La méthode des éclipses des satellites de Jupiter servit tant bien que mal jusqu'au XIXème siècle, et plutôt mal que bien. Il faut dire que la disparition d'un satellite dans l'ombre n'est pas instantanée, et que la distance parcourue dans le cône d'ombre n'est pas toujours la même. Ainsi pour la durée mise par la lumière pour parcourir la distance terre-soleil, Roemer qui avait trouvé 11 mn dans sa première estimation n'en trouva plus que 7 dans une seconde série de calculs. Cette cruelle incertitude réduit d'ailleurs à une grosse sottise l'affirmation des créationnistes qui veulent que Roemer ait mesuré la vitesse de la lumière à 200 km/s près. En réalité, en fonction des temps qu'il avait trouvé et des rayons admis pour l'orbite terrestre, on trouve des valeurs échelonnées entre 100 000 km/s et 328 000 km/s. C'est donc bien un ordre de grandeur. Cassini trouva 7 mn 5 s en 1693, Halley 8.5 minutes en 1694, et Newton 7 mn 30 s en 1704. La méthode ne semblait donc bonne qu'à fournir un ordre de grandeur. Il fallut attendre le début du XIXème siècle pour que Delambre, par la discussion d'un millier d'éclipses, étalées sur une période de 140 ans, donne la valeur de 8 mn 13 s, que nous savons aujourd'hui ètre plus correcte. Aujourd'hui, nous savons que la lumière met 8 mn 19.01 s pour parcourir le demi grand axe de l'orbite terrestre, et 8 mn 18.94 s, pour parcourir le demi petit axe Si Picard avait amené Roemer en France, c'est qu'il avait fait avec lui en 1671 un "pélerinage" à Uraniborg, c'est à dire à l'observatoire de Tycho Brahé dans l'ile de Hven, dont il fallait déterminer les coordonnées géographiques avec précision. Picard eut bien du mal à retrouver l'emplacement de l'observatoire, qui avait été détruit après le départ de Tycho. Il put néanmoins faire d'intéressantes observations et notamment observer un mouvement de l'étoile polaire d'une amplitude de 20", que Tycho n'avait pas remarqué (il ne disposait pas de lunette). Picard ne trouva aucune explication satisfaisante. L'explication allait venir au siècle suivant. L'aberration donne une mesure plus précise L'explication du phénomène observée par Picard, c'était l'aberration de la lumière, que Bradley découvrit sans la chercher, et qui débouchait sur une autre méthode de détermination astronomique de la vitesse de lumière. Depuis l'adoption du système de Copernic, on butait sur un problème. De même que la révolution terrestre autour du soleil crée des boucles dans les trajectoires apparentes des planètes (que Ptolémée représentait par des épicycles), de même les étoiles devraient paraître parcourir au cours de l'année, une boucle, plus ou moins petite selon leur distance. Or même les observations soigneuses de Tycho Brahé n'avaient rien montré de tel. Cependant si ces boucles n'étaient pas perceptibles à l'oeil nu, on pouvait espérer les observer avec un puissant instrument. James Bradley C'est dans cet esprit que Samuel Molyneux fit installer en novembre 1725, dans sa maison de Kew Green, près de Londres, un cercle zénital, fabriqué par l'habile constructeur Graham. Robert Hooke venait de prétendre avoir découvert un phénomène de parallaxe sur l'étoile gamma du dragon. qui passe presque au zénith de Londres. Molyneux laissa le soin des observations au révérend James Bradley, qui décela effectivement une variation dans la déclinaison de l'étoile... en sens inverse du mouvement attendu. Pour en avoir le coeur net, Molyneux et Bradley commandèrent au même Graham, un instrument plus performant qu'ils installèrent à Wanstead (de l'autre coté de Londres) en août 1727. Les observations de Bradley jusqu'à la fin de 1727 confirmèrent le phénomène. Ce serait lors d'un voyage sur la Tamise, en observant un drapeau flotter dans le vent relatif au bateau, que Bradley comprit ce qui se passait: cette aberration était provoquée par la combinaison du mouvement de la terre, avec celui de la lumière. Du même coup, ses mesures permettaient, soit de mesurer la vitesse de la lumière, connaissant celle de la terre, soit l'inverse. L'aberration dessinant une ellipse de 20.25 " de demi-grand axe, il en déduit que la vitesse de la lumière vaut 10 188 fois celle de la terre. A nouveau se pose le problème de la distance terre-soleil, puisque c'est à partir d'elle qu'on peut calculer la vitesse de la terre sur son orbite, mais Bradley put en déduire indépendamment que la lumière devait parcourir la distance terre-soleil en 8 mn 13 s La discussion de 3 années d'observations permit à Struve, en 1842, de donner une valeur plus exacte: 20.45". Les premières mesures de laboratoire En décembre 1838, Arago expose à l'académie le projet d'une expérience propre à trancher entre les deux théories de la lumière: la théorie corpusculaire de l'émission (Newton) et le théorie des ondulations (Huygens et Fresnel). Arago compte utiliser un dispositif à miroir tournant concu par Wheatstone, où deux rayons parallèles traverseraient un milieu différent. Il explique: François Arago "Selon la théorie de l'émission, la lumière se meut dans l'eau notablement plus vite que dans l'air. Selon la théorie des ondes, c'est précisément le contraire: la lumière marche plus vite dans l'air que dans l'eau. Faisons en sorte qu'avant d'arriver au miroir, un des deux rayons, le rayon supérieur, par exemple, ait à traverser un tube rempli d'eau. Si la théorie de l'émission est vraie, ce rayon supérieur sera accéléré dans sa marche; il se réfléchira avant le rayon inférieur; il formera avec lui un certain angle, et le sens de la déviation sera tel, que le rayon inférieur paraîtra plus avancé que l'autre, qu'il semblera avoir été entrainé plus vite par le miroir tournant. Tout restant égal, admettons un moment la vérité du système des ondes. Le tube d'eau retardera alors la marche du rayon supérieur; ce rayon arrivera au miroir réfléchissant après le rayon inférieur; il se réfléchira, non plus le premier, comme tout à l'heure, mais le second, ..." Cette expérience d'Arago ne fut jamais réalisée. Le dispositif de Wheatstone nécessitait une trop grande longueur entre le miroir tournant et l'observateur, et utilisait des éclats lumineux dont on ne savait où il fallait les détecter. Ce projet allait pourtant inspirer l'expérience de Foucault En 1849, Hippolyte Fizeau utilise une roue dentée, dont l'axe est parallèle à un faisceau lumineux. Lorsque le faisceau n'est pas arrêté par une «dent» de la roue, il est renvoyé par un miroir placé à grande distance, comme l'avait suggéré Fermat pour Galilée. Quand le rayon revient sur la roue, soit il passe entre deux dents, soit il est arrété par une dent, selon la vitesse de la roue. On observe alors une éclipse pour une certaine vitesse, une réapparition du signal lumineux pour une vitesse double, une nouvelle éclipse pour une vitesse triple, etc.. 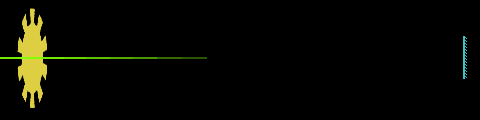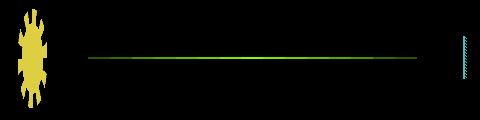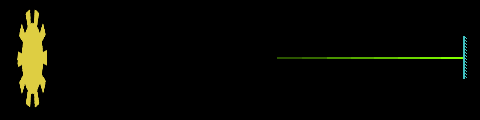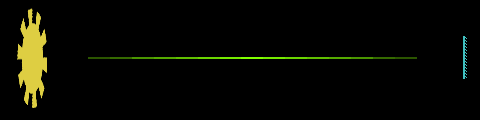principe de la roue dentée En opérant de nuit, sur une distance de 8 633 m entre Suresnes et Montmartre, la moyenne de 28 observations lui donne une valeur d'environ 315 000 km/s. Ce n'est pas mieux que les méthodes astronomiques, mais c'est la première fois qu'on réalise une mesure "de laboratoire", donnant directement la valeur cherchée sans dépendre d'une autre grandeur, comme la distance terre-soleil. Si Galilée avait été là, il en eut peut-être pleuré de joie. Mais remarquons que, si Fizeau réussit là où Galilée échouat, c'est qu'il connaissait, lui, l'ordre de grandeur de qu'il voulait mesurer. Sans Roemer et Bradley, Fizeau eut du faire plusieurs expériences, négatives, en augmentant la distance, avant de réussir... 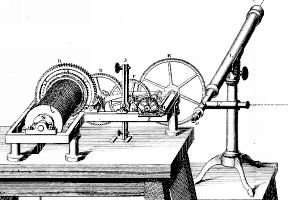ou de se décourager Hippolyte Fizeau La machine à roue dentée Léon Foucault A partir de 1850, Léon Foucault perfectionne la méthode du miroir tournant de Wheatstone et Arago, en introduisant un second miroir. Plus sensible que la roue dentée grâce à son miroir entraîné à grande vitesse par une turbine, cette méthode lui permet de diminuer la distance nécessaire entre les miroirs et d'opérer à l'intérieur même du laboratoire. Pour une déviation fixée du rayon lumineux, la vitesse de rotation du miroir permet de calculer la vitesse de la lumière, connaissant la longueur du parcours aller retour entre le miroir tournant et le miroir fixe. En 1850 il peut ainsi réaliser l'expérience de comparaison des vitesses dans l'air et dans l'eau, et montrer que la lumière se déplace moins vite dans l'eau, en accord avec la théorie des ondulations En 1862, avec un miroir tournant à 400 tr/s il obtient pour la vitesse de la lumière la valeur de 298 000 km/s 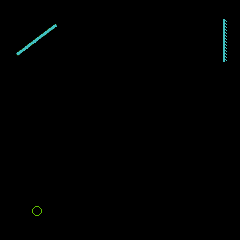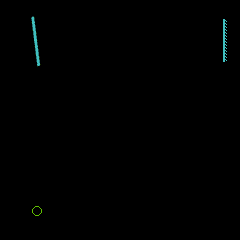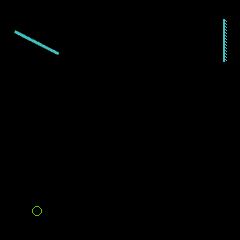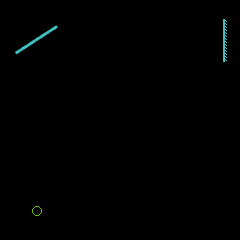principe du miroir tournant le miroir de Foucault, avec la turbine de Gustave Froment La multiplication des méthodes Alfred Cornu A partir de 1870 Alfred Cornu reprend la méthode de la roue dentée en la perfectionnant. Il imagine de détecter des intensités égales de part et d'autres de l'extinction du signal, et d'opérer un enregistrement électrique de la vitesse de la roue. Une première mesure sur une distance de 10 310 m entre l'école polytechnique et le Mont Valérien lui donne une valeur 298 500 km/s avec une erreur estimée de moins de 1/100 soit moins de 3000 km/s. En 1874 à l'instigation de Leverrier et Fizau, il entreprend une expérience plus précise entre deux sommets de la triangulation de Cassini distants de 23 910 m : l'observatoire et la tour de Monthéry. Il obtient la valeur de 300 400 Km/s L'erreur qu'il commet est de 608 km/s. Mais bien sûr, cette erreur, il ne la connaît pas. Cependant il estime l'erreur probable inférieure à un millième en valeur relative, soit 300 Km/s. Il est un des premiers à donner une marge d'erreur. Il ne sera pas le dernier à échouer à donner une marge qui contienne la valeur correcte L'heure n'est plus guère aux déterminations astronomiques dont la meilleure méthode, celle de l'aberration, plafonne à une précision d'environ 1/2000, mais aux mesures de laboratoire. Plusieurs méthodes s'affrontent pour déterminer avec le plus de précision possible, cette vitesse de la lumière, qu'on note c (du latin céléritas = vitesse): - La roue dentée, qui va bienôt déclarer forfait, et sera remplacée par la cellule de Kerr - Le miroir tournant, qui va encore être perfectionné - les mesures de la vitesse des ondes électriques, dont Maxwell a démontré qu'elle est identique à la vitesse de la lumière dans le vide. Ces mesures ne feront pas mieux que les mesures astronomiques jusqu'à la fin du XIXème siècle Mais toutes ces méthodes vont donner un corpus de valeurs disparates, où les plages d'incertitudes se recoupent mal. Il faut dire que le paramètre d'erreur "probable" est basé sur "l'écart réduit" des différentes mesures, pour un intervalle de confiance de 50% seulement. Il y a donc une chance sur deux que la vraie valeur soit à l'extérieur de l'intervalle donné Albert A. Michelson En 1878 Albert Michelson, alors âgé de 25 ans entre en scène. Il "bricole" une expérience q'il décrit à Newcomb (on dit qu'elle ne lui avait coûté que quelques dollars). Michelson utilise la méthode du miroir tournant. Avec seulement 10 mesures et une base de 152 m, il trouve 300 140 ± 480 km/s. Cette mesure "d'amateur" vaut largement celle de Cornu. En 1879, avec 100 mesures et une base de 605 m, Il trouve une valeur de 299 910 km/s ± 50 km/s. Là encore la valeur actuellement connue n'est pas dans la plage d'incertitude. Cependant Michelson va améliorer ses méthodes et régner pendant 50 ans sur l'instrumentation à miroir. Son savoir-faire lui permettra de monter en 1887, avec Edward Morley, la célèbre expérience mettant en défaut la théorie de l'éther électromagnétique. Il aura le prix Nobel en 1907 En 1880 Young et Forbes, avec une roue dentée mesurent 301 382 Km/s, et croient trouver une dispersion de 1.8% selon la longueur d'onde, résultat qui ne sera pas confirmé En 1882 Newcomb, avec le miroir tournant et une base de 3721 m, trouve 299,860 km/s ±30 (toujours à côté) Michelson, lui, trouve 299 853 km/s ±60 km/s ( à 500 m/s près, il avait bon) En 1891 Blondlot (l'homme des rayons N) mesure des ondes stationnaires dans des fils électriques, il trouve 302 200 km/s, puis 297 200 km/s deux ans plus tard La roue dentée est utilisée une dernière fois en 1900 par Perrotin. En 1902 il trouve 299 860 km/s ±80 km/s, ce qui vaut les résultats de Newcomb et Michelson 20 ans auparavant La roue dentée, bètement mécanique, va alors céder la place à un commutateur électro-optique, la cellule de Kerr, qui permettra aussi les débuts de la télévision Ce n'est qu'en 1906, que Rosa et Dorsey trouvent enfin une valeur précise par la comparaison des unités électromagnétiques et électrostatiquesIls auraient obtenu 299 710 km/s ± 22 km/s ( la source, Bulletin of the Bureau of Standards, Vol. 3, n'est pas accessible en ligne) En 1923 La méthode de Blondlot permet à Mercier d'obtenir 299 795 km/s ± 30 km/s Les dernières (et les meilleures) mesures de Michelson eurent lieu en 1926 sur une base de 35 km, entre le mont Wilson et le mont San Antonio. Avec des miroirs à 8, 12 et 16 faces, tournant à 528 t/s, il obtient la valeur de 299 796 km/s ±4 km/s. 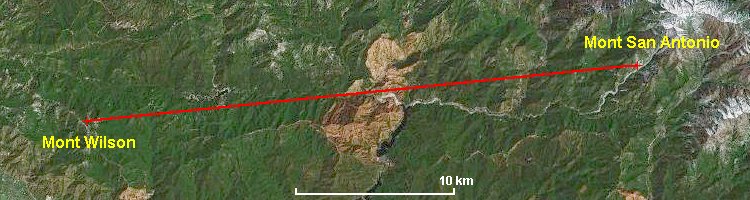Non seulement la plage d'incertitude est réduite, mais nous savons aujourd'hui que la valeur correcte est dedans 35 km, la plus longue base jamais utilisée Le temps du doute Le tube de 1 mile Pouvait on faire mieux? Michelson imagina de faire l'expérience dans le vide. En 1930 il entreprit de faire construire près de Pasadéna, un tube en acier d'un mile de long pour y faire une ultime expérience. Il mourut en 1931 sans en voir les résultats. Peut ètre valait il mieux, car les dits résultats déçurent toutes les attentes Ce fut un des premiers grands échecs de la "Big science". En dépit du soin apporté à la construction du tube, à mesurer la longueur de la base et à maintenir moins de 1/100 d'atmosphère dans le tube, les valeurs mesurées s'obstinaient à varier de façon imprévisible, sautant de 50 km/s d'une mesure à l'autre. Les continuateurs de l'expérience de Michelson, Pease et Pearson, furent bien embarrassés en présentant leur résultat en 1935: 299 774 km/s ±11 km/s, encore ce résultat était-il optimiste car les 493 mesures de 1931 donnaient 299 770, et les 753 mesures de 1932 donnaient 299 780. Bien qu'on ait vérifié la longueur du tube, ils en invoquèrent une variation en fonction du coefficient de marée, et présentèrent même un diagramme des résultats en fonction de la dimension apparente de la lune! 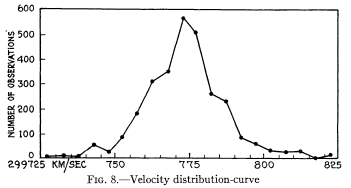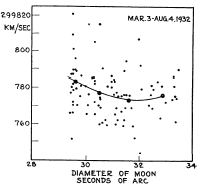(ce diagramme est révélateur de la compétence des expérimentateurs qui confondent les minutes et les secondes d'arc) distribution des valeurs trouvées tentative d'explication lunaire 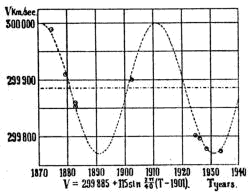Entretemps, Karolus et Mittelstaedt, avec un dispositif à cellule de Kerr avaient, en 1928, obtenu un résultat, au moins aussi bon, avec une installation beaucoup moins coùteuse: 299 786 km/s ±10 km/s (la valeur correcte est bien dans la marge) variation de c selon Gheury de Bray Que signifiait cette salade de résultats? Pour nous, qui connaissons la valeur précise, elle ne fait que révéler l'imprécision des mesures de l'époque, mais le doute s'était installé dès 1927, sous la plume de M.E.J. Gheury de Bray, qui dans Nature et dans L'astronomie défendit l'idée que ces mesures trahissaient une diminution de c avec le temps Cette théorie qui eut des échos dans des revues françaises, fut âprement discutée pendant une dizaine d'années dans les colonnes de Nature. Il faut dire que M.E.J. Gheury de Bray semblait ignorer le problème de l'incertitude des mesures, choisissait les mesures qui l'arrangeaient, et finit même par changer de théorie en 1934: La vitesse de la lumière fluctuait sinusoïdalement! Cette "théorie" n'appartient plus qu'au musée des idées fausses, cependant l'idée d'une variation de c avec le temps n'est pas morte, comme nous le verrons plus loin. D'ailleurs, pour les "créationnistes" qui croient à l'infinitude la la vitesse de la lumière il y a 6000 ans, M.E.J. Gheury de Bray est un précurseur Le temps de la précision 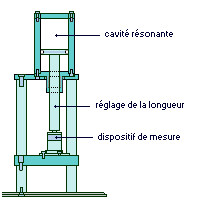La cavité résonante de Essen On comprend qu'entre 1940 et 1945, les physiciens aient eu autre chose à faire que de mesurer la vitesse de la lumière avec la meilleure précision possible. Mais à partir de 1947, de nouvelles technologies de plus en plus "pointues" vont permettre de dépasser la référence de précision des mesures de longueur. Ce sont le radar, le géodimètre et le telluromètre (utilisé par les arpenteurs et les géodésiens), la cavité résonnante, le radio-interféromètre, la spectrométrie de bande, et, last but not least, le laser La cavité résonante est un guide d'onde fermé dont on mesure la fréquence de résonance. En 1947, avec une cavité à Longueur variable, Louis Essen trouve 299 792 km/s ±3 km/s Avec la technique du radar, en 1949, C.I Aslakson mesure 299 792.4 ±2.4 km/s. L'incertitude passe sous la barre de 1/100 000 La même année Erik Bergstrand avec un géodimètre à oscillateur à quartz et cellule de Kerr, trouve 299 793 km/s ±2 km/s En 1950, à Stanford, avec une cavité résonante de longueur fixe, Hansen et Bol trouvent 299 794.3 km/s ±1.2 km/s 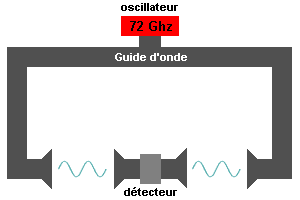shéma du radio-interféromètre de Froome En 1951 Keith Davy Froome avec un radio interféromètre à ondes millimétriques trouve 299 792.6 ±0.7 km/s En 1954 Avec la spectrométrie de bande, Rank n'arrive qu'à 299 789 km/s ±3 km/s, puis 299 791.9 km/s ±2.2 km/s, l'année suivantre. Mais en cette année 1954, Froome en est à 299 792.75 km/s ±0.3 km/s En 1956 avec son telluromètre Wadley ne fait pas mieux que 299 792.7 km/s ±2. km/s En 1958 Froome atteint 299 792.5 km/s ±0.1 km/s. C'est la meilleure mesure avant l'entrée en scène du laser Les mesures atteignent la limite de précision du vieux mètre étalon en platine iridié. En 1960 la 11ème conférence des poids et mesures, prenant acte que le prototype international ne définit plus le mètre avec une précision suffisante pour les besoins de la métrologie d'alors, rédéfinit le mètre: « Le mètre est la longueur égale à 1 650 763,73 longueurs d'onde dans le vide de la radiation correspondant à la transition entre les niveaux 2p10 et 5d5 de l'atome de krypton 86.. » type de laser hélium-néon stabilisé Mais la précision atteinte fait un bond d'un facteur 100 avec l'utilisation du laser. En 1972, Kenneth Evenson et son équipe du National Institute of Standards and Technology utilise un laser hélium-néon stabilisé et obtiennent 299 792.4574 km/s ±0.0011 km/s (ils y gagnent une médaille d'or du Department of Commerce) En 1978, Woods, Shotton et Rowley atteignent 299 792.45898 km/s ±0.0002 km/s C'est à dire que la vitesse de la lumière est maintenant connue à 20 cm/s près! A nouveau la précision du mètre étalon n'est plus suffisante. Solution: renverser la définition en ne définissant plus la vitesse de la lumière par rapport au mètre, mais l'inverse. Le 20 octobre 1983, la 17ème conférence des poids et mesures décide : « Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299792458 s. » La course à la précision s'arrète la. La vitesse de la lumière est maintenant exacte et constante... par définition. Le temps des interrogations Mais voila, si c est constante d'après le modèle physique standard, ce n'est jamais qu'un modèle. On sait que La constance de c étant reliée aux autres paramètres du modèle, il est impossible d'y toucher, en laissant identiques ces autres paramètres, car cela créerait une incohérence dimensionnelle. Mais cela n'impose pas cette constance dans l'absolu. Simplement, une variation de c n'est possible que dans le cadre d'une cosmologie "alternative" ou les invariants fondamentaux ne sont plus les mêmes. Le problème c'est qu'il n'est théoriquement plus possible de trancher par l'observation, avec les étalons d'aujourd'hui. A l'époque ou M.E.J. Gheury de Bray défendait l'idée d'une variation, la précision des mesures ne permettait pas de vérifier une variation avec le temps cosmologique. En effet, la constante de Hubble valant environ .02 m/s par année.lumière, une interprétation du décalage vers le rouge des galaxies en terme de variation de la vitesse de la lumière ne faisait jamais qu'une variation de 6 m/s depuis Ole Roemer. Aujourd'hui, depuis 32 ans qu'on sait mesurer la vitesse de la lumière à 20cm/s près, cela ferait une vriation de 0.6 m/s, donc théoriquement mesurable. Mais voila le mètre est maintenant défini par rapport à c, et la seconde, par rapport à un intervalle de fréquence: « La seconde (s) est la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l'état fondamental de l'atome de césium 133.. » Si on admet que la fréquence est un invariant et que la seconde reste constante, il n'en reste pas moins, que même si c doublait, sa mesure donnerait encore 299 792 458 m/s, puisque le mêtre aurait doublé! Il faudrait donc refaire des mesures avec les mêmes étalons qu'en 1978, la précision des lasers stabilisés ne pouvant qu'avoir augmenté, la comparaison avec la résultat de 1978 permettrait de trancher. Non pas en prouvant la constance absolue de la vitesse de la lumière, qui pourrait être sujette à des variations non mesurables, mais en validant ou invalidant l'hypothèse d'une variation avec le temps cosmologique. La difficulté est que la définition du mètre, utilisée en 1978, n'avait pas une précision suffisante, utilisant neuf chiffres quand il en eut fallu dix. Mais peut être que l'étalonnage du laser stabilisé, lui, était suffisamment précis. Le temps des bétises Le bêtisier ↑ lire le dossier ↑ Mais si la variation de c avec le temps cosmologique mérite encore d'ètre testé, d'autres modèles ne le méritent pas. Nous avons déja vu le modèle à géométrie variable de M.E.J. Gheury de Bray, mais il y a pire. Dans le cadre d'un univers très, très jeune, puisqu'il n'a guère plus de 6000 ans, les créationnistes américains ont pris la variation de c comme cheval de bataille. Pour eux, les mesures d'il y a plusieurs siècles prouvent la décroissance rapide de c. Et cette décroissance leur permet de manipuler la chronologie et de faire retomber le chronologie biblique sur ses pattes Quand aux islamistes, ils ne sont pas en reste et prétendent trouver la valeur précise de la vitesse de la lumière dans le coran. Il faut dire qu'ils y trouvent aussi la contraction relativiste, les pulsars, les quasars, les trous noirs, les trous de vers, la matière noire... bref, tout Ainsi, non seulement le problème de la variation de c est quasiment interdit d'expérience, mais il est discrédité. Pourtant il n'y a aucun rapport entre les modèles alternatifs à variation de c (infime) et les stupidités créationnistes. Mais on peut penser que la lutte, contre l'obscurantisme créationniste, a favorisé l'existence d'un front pour la constance de c, qui peut faire penser à celui des philosophes pour l'infinitude de c, d'Aristote à Descartes.